I don't understand this explanation for \sum_(n=0)^\infty((-1)^n)/(5n-1)∞∑n=0(−1)n5n−1? Why test for convergence/divergence AGAIN, if the Limit Comparison Test confirms that both series are the same?
"First we will check whether the series is absolutely convergent.
Because If the series is absolutely convergent then the series is convergent.
But if the series is not absolutely convergent. Then we will check whether the series is convergent or divergent."
 slader
slader
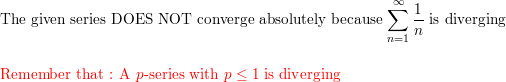 slader
slader
 slader
slader
 slader
slader
"First we will check whether the series is absolutely convergent.
Because If the series is absolutely convergent then the series is convergent.
But if the series is not absolutely convergent. Then we will check whether the series is convergent or divergent."
 slader
slader
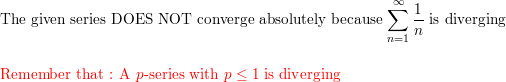 slader
slader
 slader
slader
 slader
slader
1 Answer
The series only converges conditionally. It is possible to have
Explanation:
The Limit Comparison Test, when applied to this problem, tells us that the absolute value of the series,
However, it is totally possible to have
This is called conditional convergence , and we must always check for it.
There is no "absolute divergence" that tells us if the absolute value of the series diverges, so must the series itself.
So, if
Now, we can say
Now, using the Limit Comparison Test,
So, both series must diverge.
Now, the original series,
Now, the positive, non-alternating portion of
The Alternating Series Test tells us if

