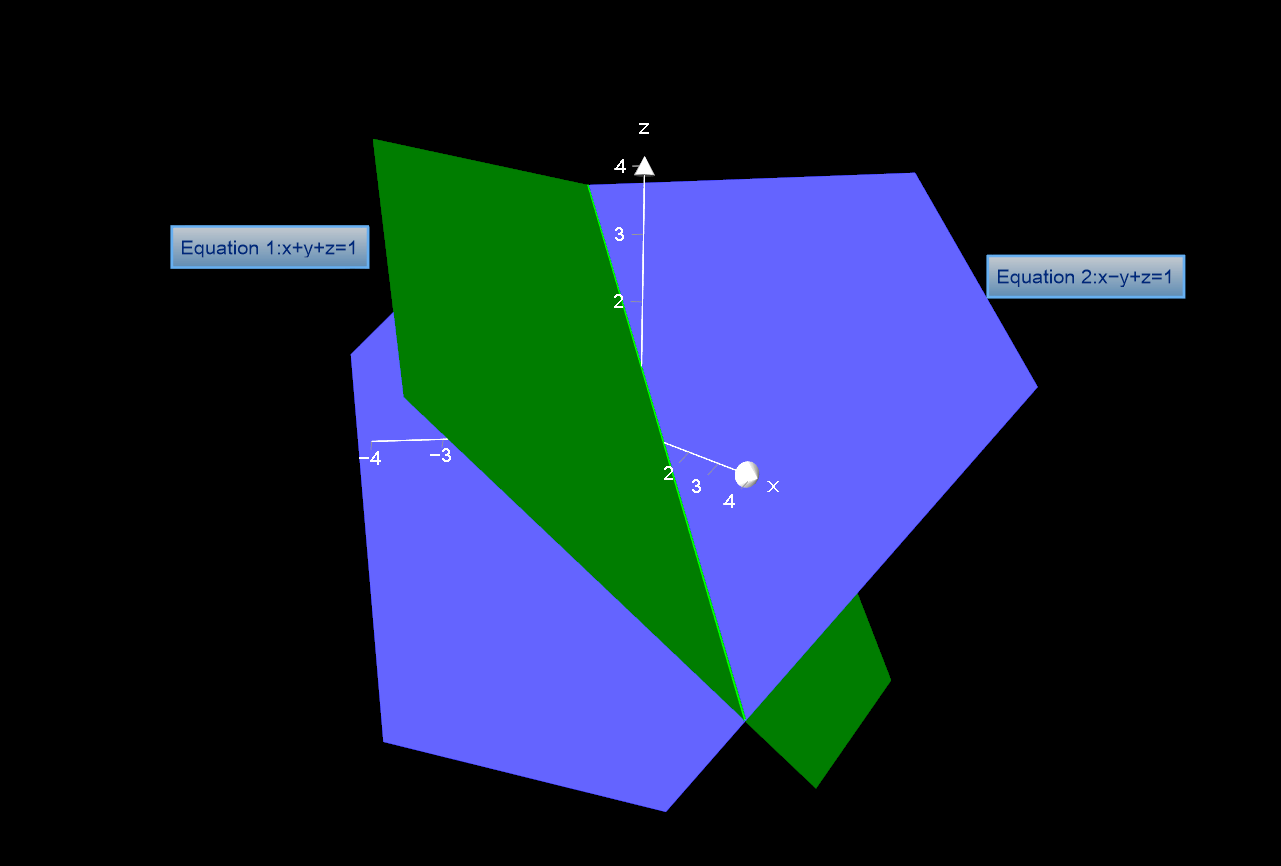
Are the planes #x+y+z=1# , #x-y+z=1# parallel, perpendicular, or neither? If neither, what is the angle between them?

Question

7411 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-04-20T14:53:57

#color(blue)("Neither")#

We can find the angle between two planes, by finding the angle between the normals to the plane:

When given the equation of a plane in Cartesian form:

#ax+by+cz=d#

The normal vector to the plane is:

#vec(bbn)=((a),(b),(c))#

Let:

#Pi_1=x+y+z-1=0#

#Pi_2=x-y+z-1=0#

Then:

#vec(bbn_1)=((1),(1),(1))#

#vec(bbn_2)=((1),(-1),(1))#

We can find the angle between these normals using the Dot Product:

#bb(n_1*n_2)=||bb(n_1)||*||bb(n_2)||*cos(theta)#

#bb(n_1*n_2)=1#

#||bb(n_1)||=sqrt((1)^2+(1)^2+(1)^2)=sqrt(3)#

#||bb(n_2)||=sqrt((1)^2+(-1)^2+(1)^2)=sqrt(3)#

#1=sqrt(3)*sqrt(3)*cos(theta)#

#cos(theta)=1/(sqrt(3)*sqrt(3))=1/3#

#theta=arccos(1/3)=70.53^@# 2 d.p.

If the planes were perpendicular, the the angle between them would be #90^@#.

If the planes were parallel, the the angle between them would be #0^@#. Therefore they are neither.

Plot:

enter image source here