Please help right triangles??
A 50-foot ladder leans against a wall so that it is 40 feet high at the top. The ladder is moved so that the base of the ladder travels toward the wall twice the distance that the top of the ladder moves up. How much higher is the top of the ladder now? (Hint: Let 30−2x be the distance from the base of the ladder to the wall.) 
A 50-foot ladder leans against a wall so that it is 40 feet high at the top. The ladder is moved so that the base of the ladder travels toward the wall twice the distance that the top of the ladder moves up. How much higher is the top of the ladder now? (Hint: Let 30−2x be the distance from the base of the ladder to the wall.) 
2 Answers
It is impossible to move the ladder with that ratio!
Explanation:
We have a "standard" 3-4-5 right triangle. The hypotenuse (50) doesn't change. Per the "hint" the bottom movement may be written as 30 - 2x for a top movement of 40 + x. The movement 'x' cannot be greater than 10 (vertical ladder).
Combining these in the Pythagorean Theorem we obtain:
It cannot be moved in that ratio!
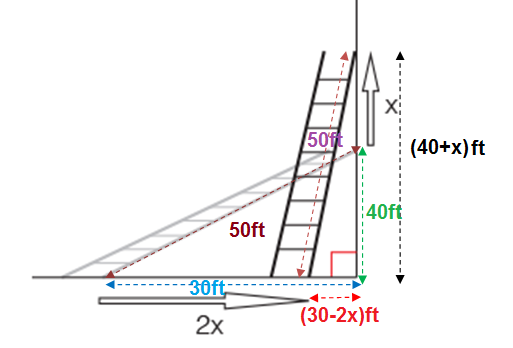
Let (30−2x) ft be the distance from the base of the ladder to the wall.
Initially height of the top of the ladder
From the figure by Pythagoras theorem we have
So final height of the top of the ladder


