Question

An isosceles triangle has sides A, B, and C with sides B and C being equal in length. If side A goes from `(1 ,4 )` to `(5 ,1 )` and the triangle's area is `15`, what are the possible coordinates of the triangle's third corner?

Answer 1

The two vertices form a base of length 5, so the altitude must be 6 to get area 15. The foot is the midpoint of the points, and six units in either perpendicular direction gives `(33/5, 73/10)` or `(- 3/5 , - 23/10 )`.

Explanation:

Pro tip: Try to stick to the convention of small letters for triangle sides and capitals for triangle vertices.

We're given two points and an area of an isosceles triangle. The two points make the base, `b=\sqrt{(5-1)^2+(1-4)^2}=5.`

The foot `F` of the altitude is the midpoint of the two points,

`F = ( (1+5)/2, (4+1)/2 ) = (3, 5/2)`

The direction vector from between the points is `(1-5, 4-1)=(-4,3)` with magnitude 5 as just calculated. We get the direction vector of the perpendicular by swapping the points and negating one of them: `(3,4)` which must also have magnitude five.

Since the area `A=\frac 1 2 b h = 15` we get `h=(2*15)/b=6.`

So we need to move `6` units from `F` in either perpendicular direction to get our third vertex which I've called `C`:

`C = F \pm 6 \frac{ (3,4) }{5} = (3, 5/2) \pm 6/5 (3,4)`

`C = (33/5, 73/10) or C=(- 3/5 , - 23/10 )`

Check: `(5,1)-(1,4)=(4,-3)`
`(- 3/5 , - 23/10 )-(1,4)=(-8/5,-63/10)`
The signed area is then half the cross product

`A=frac 1 2( 4(-63/10) - (-3)(-8/5) ) = -15 \quad\sqrt{}`

---

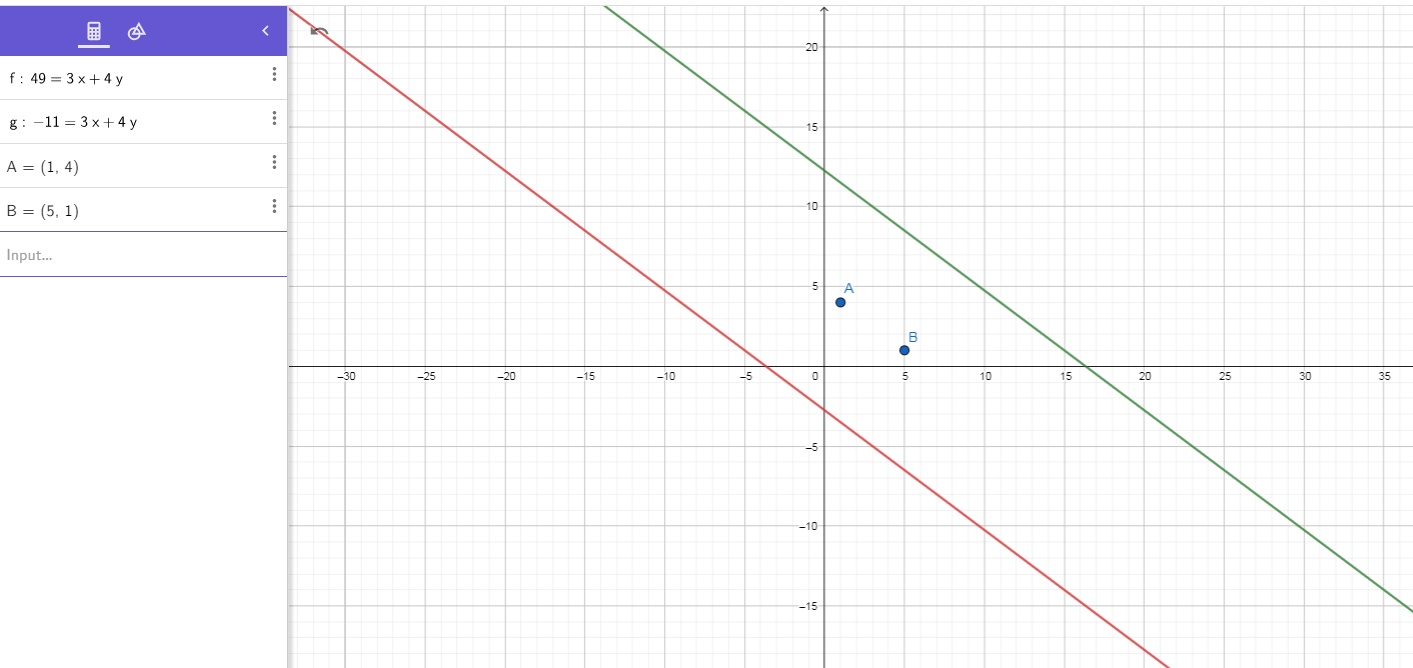
That's the end, but let's generalize the answer a bit. Let's forget about it being isosceles. If we have C(x,y), the area is given by the shoelace formula:

`A = \frac 1 2 | (1)(1)-(4)(5) + 5y-x + 4x-y | = 1/2 | 3x+4y - 19|`

The area is `15`:

`\pm 15 = 1/2 ( 3x+4y - 19 )`

`19 \pm 30 = 3x + 4y`

`49=3x+4y` or `-11=3x+4y`

So if the vertex C is on either of those two parallel lines, we'll have a triangle of area 15.

Answer 2

Let `PR=A` be the side of the isosceles triangle having coordinates of its end points as follows

`Pto(1,4)` and `Rto (5,1)`

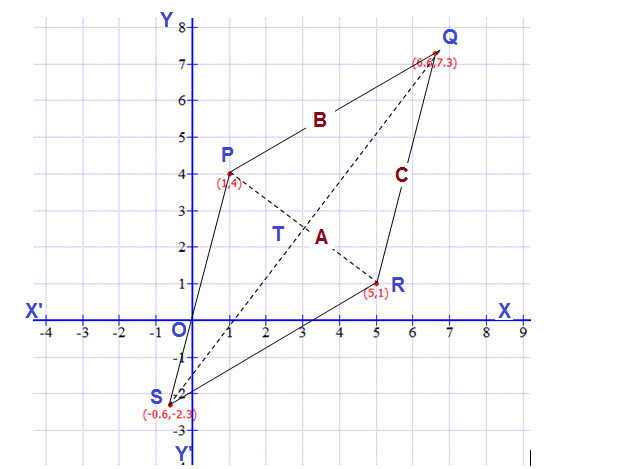Let the coordinates of the third point of the triangle be `(x,y)`.

As `(x,y)` is equidistant from P and R we can write

`(x-1)^2+(y-4)^2=(x-5)^2+(y-1)^2`

`=>x^2-2x+1+y^2-8y+16=x^2-10x+25+y^2-2y+1`

`=>8x-6y=9`

`=>x=(9+6y)/8......[1]`

Again `(x,y)` being equidistant from P and R, the perpendicular dropped from `(x,y)` to `PR` must bisect it, Let this foot of the perpendicular or mid point of `PR` be `T`

So coordinates of `Tto(3,2.5)`

Now height of the isosceles triangle

`H=sqrt((x-3)^2+(y-2.5)^2)`

And the base of the isosceles triangle

`PR=A=sqrt((1-5)^2+(4-1)^2)=5`

So by the problem its area

`1/2xxAxxH=15`

`=>H=30/A=30/5=6`

`sqrt((x-3)^2+(y-2.5)^2)=6`

`=>(x-3)^2+(y-2.5)^2=36....[2]`

By [2] and [1] we get

`((9+6y)/8-3)^2+(y-2.5)^2=36`

`=>1/64(6y-15)^2+(y-2.5)^2=36`

`=>(6y-15)^2+64(y-2.5)^2=36xx64`

`=>36y^2-180y+225+64y^2-320y+400=48^2`

`=>100y^2-500y+625=48^2`

`=>y^2-5y+6.25=4.8^2`

`=>(y-2.5)^2=4.8^2`

`=>y=2.5pm4.8`

So `y=7.3 and y= -2.3`

when `y=7.3`

`x=(9+6xx7.3)/8=6.6`

when `y=-2.3`

`x=(9+6xx(-2.3))/8=-0.6`

So the coordinates of third point will be

`(6.6,7.3)to"Q in figure"`

OR

`(-0.6,-2.3)to"S in figure"`