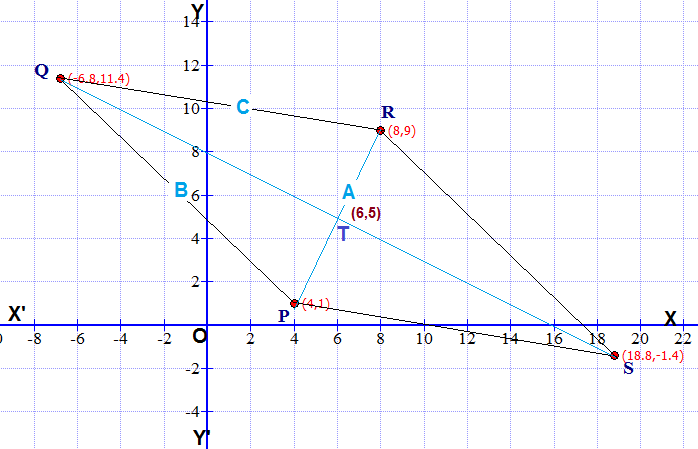
 Let #PR=A# be the side of the isosceles triangle having coordinates of its end points as follows
Let #PR=A# be the side of the isosceles triangle having coordinates of its end points as follows
#Pto(4,1)# and #Rto (8,9)#
Let the coordinates of the third point of the triangle be #(x,y)#.
As #(x,y)# is equidistant from P and R we can write
#(x-4)^2+(y-1)^2=(x-8)^2+(y-9)^2#
#=>x^2-8x+16+y^2-2y+1=x^2-16x+64+y^2-18y+81#
#=>8x+16y=128#
#=>x+2y=16#
#=>x=16-2y......[1]#
Again #(x,y)# being equidistant from P and R, the perpendicular dropped from #(x,y)# to #PR# must bisect it, Let this foot of the perpendicular or mid point of #PR# be #T#
So coordinates of #Tto(6,5)#
Now height of the isosceles triangle
#H=sqrt((x-6)^2+(y-5)^2)#
And the base of the isosceles triangle
#PR=A=sqrt((4-8)^2+(1-9)^2)=4sqrt5#
So by the problem its area
#1/2xxAxxH=64#
#=>H=128/A=128/(4sqrt5)=32/sqrt5#
#sqrt((x-6)^2+(y-5)^2)=32/sqrt5#
#=>(x-6)^2+(y-5)^2=1024/5=204.8....[2]#
By [2] and [1] we get
#(16-2y-6)^2+(y-5)^2=204.8#
#=>(10-2y)^2+(y-5)^2=204.8#
#=>5y^2-50y+125==204.8#
#=>y^2-10y+25==40.96#
#=>(y-5)^2=6.4^2#
#=>y=5pm6.4#
So #y=11.4 and y= -1.4#
when #y=11.4#
#x=16-2xx11.4=-6.8#
when #y=-1.4#
#x=16-2xx(-1.4)=18.8#
So the coordinates of third point will be
#(-6.8,11.4)to"Q in figure"#
OR
#(18.8,-1.4)to"S in figure"#
 Let
Let 
