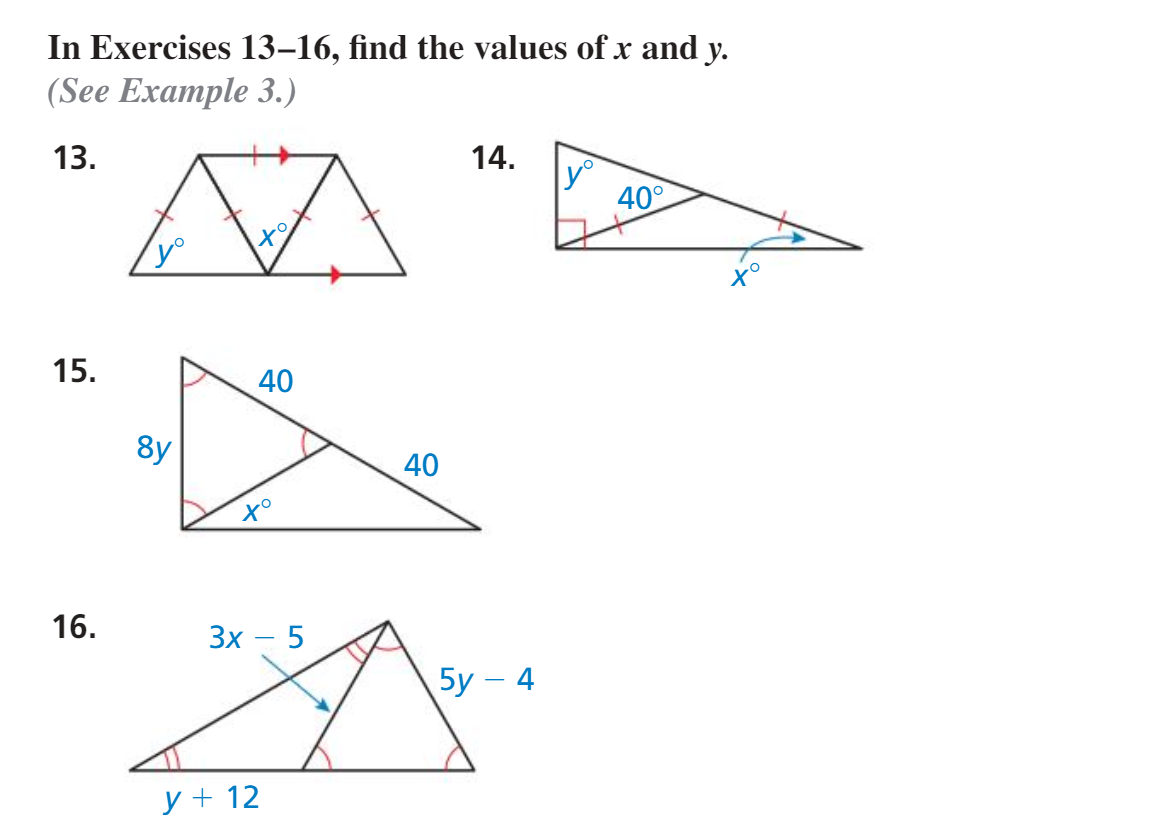
14:
the angle to the right of the #40^@# angle adds to #40^@# to make #180^@#, since both angles lie on the same straight line.
the angle to the right of the #40^@# angle is therefore #140^@#.
it is shown that #x# is a base angle of an isosceles triangle, meaning that the angle opposite to it is also the size of #x#.
we know that the top angle in the triangle is #140^@#. since the sum of angles in a triangle is #180^@#, it is known that #x+x# is #40^@#, and that #x# is therefore #20^@#.
the angle to the left of #x# is #70^@#, since #x# is #20^@# and both angles add to the size of a right angle #90^@#.
#y# is the remaining angle in the triangle with angles #40^@# and #70^@#. the sum of angles in a triangle is #180^@#, so #y = 180^@ - 40^@ - 70^@#, which is #70^@#.
15:
the left triangle is shown to have all its angles equal. this is an equilateral triangle with all its sides and angles equal.
here, all its sides have length #40#. #8y# is one of the sides of the triangle, so #8y = 40#, and #y = 40/8# or #5#.
the side of the equilateral triangle not labelled in blue is also length #40#. this means that the second triangle has two equal sides of length #40# and is therefore isosceles.
the top angle of the second triangle is #180^@ - 60^@#, or #120^@#, since #60^@# is the size of any angle in an equilateral triangle.
this means that the remaining angles #x + x# add to #60^@#, and that #x# is therefore #30^@#.
16:
the triangle to the left is isosceles, meaning that two of its sides are equal. these are the sides adjacent to the largest angle. their lengths are #3x - 5# and #y + 12#, meaning that #3x - 5 = y + 12#.
#3x - 5# and #5y + 4# also happen to be sides of an equilateral triangle, meaning that #3x - 5 = 5y + 4#.
we can first solve the equation where #y + 12 = 5y + 4# (since these both equal #3x - 5#):
#y + 12 = 5y - 4#
#12 = 4y - 4#
#4y = 16#
#y = 4#.
then you can figure out #y + 12#, which is #16#.
#y +12 = 3x - 5#, so #3x - 5 = 16#.
#3x - 5 =16#
#3x = 21#
#x = 7#.