The region bounded by the curve y=ln(x)/x and the lines x=1, x=e, y=0 is rotated around x=2π. Find the volume of the solid generated. How would I go about solving this? Doesn’t the integral need to be in terms of y, but ln(x)/x does not have a inverse.
1 Answer
See below
Explanation:
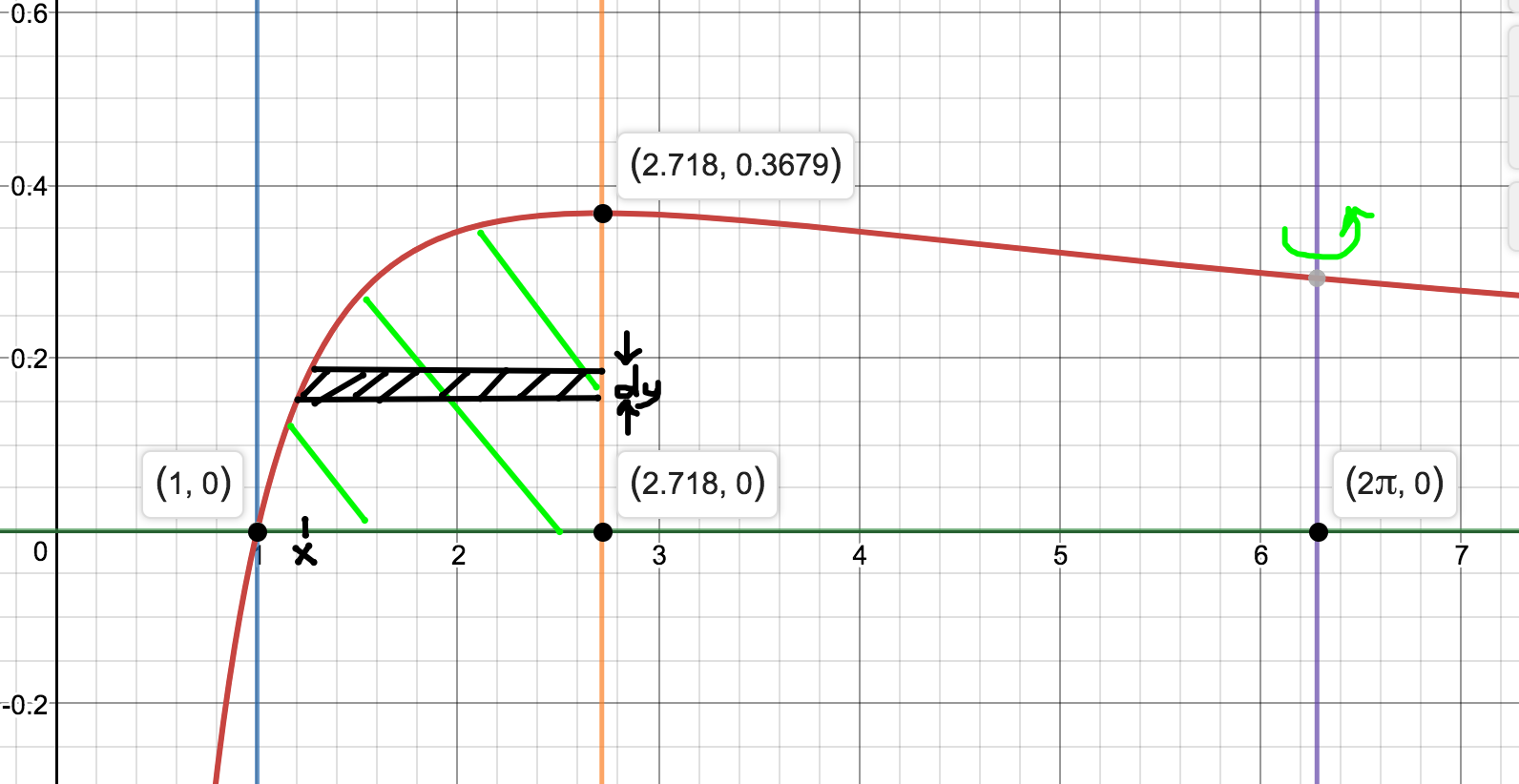
If you do it this way:
The integral is:
You don't need an inverse. That's a machine result. I'm not sure I fancy the slog of doing it by hand but it is very do-able.
If you do it this way:
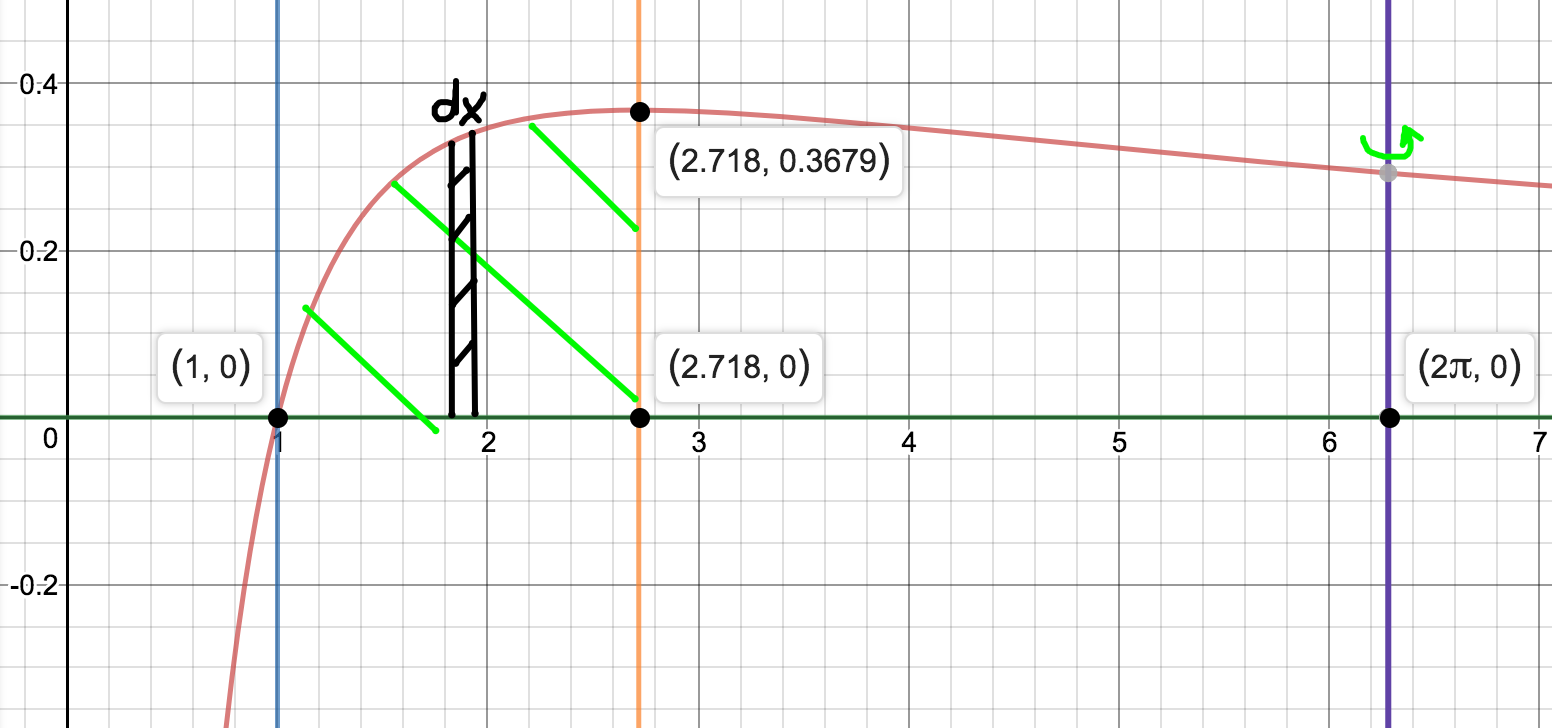
The integral is:
These results are trivial:
-
#int \ dx \ (ln x)/x = (ln^2 x)/2 + C# -
#int \ dx \ ln x = x ln x - x + C#

