How do we prove the projection law using vectors?
2 Answers
Let
So
Now vector projection of
To prove for
Proof
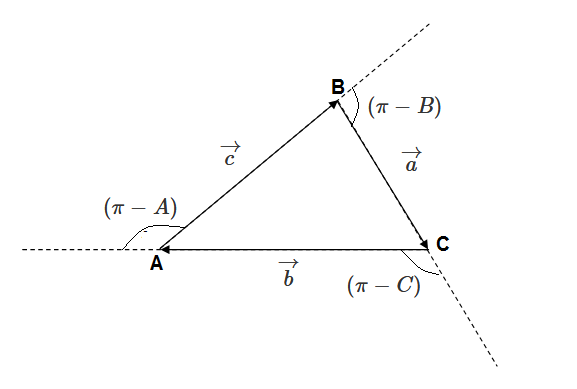
Let us consider that three vectors
This means
So we can write
Let
So
Now vector projection of

To prove for
Proof
Let us consider that three vectors
This means
So we can write