Question

For what values of x is `f(x) = -sqrt(x^3-9x^2` concave or convex?

Answer 1

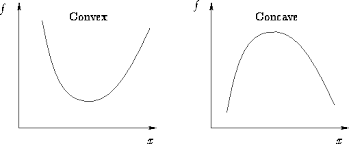
It is concave if the second derivative is less than zero and convex if the second derivative is greater than zero. "How to" is below, numeric solution is left to the student.

Explanation:

An inflection point is a point on a curve at which the sign of the curvature (i.e., the concavity) changes. Inflection points may be stationary points, but are not local maxima or local minima. For example, for the curve `y = x^3`, the point `x=0` is an inflection point.

First Derivative Test

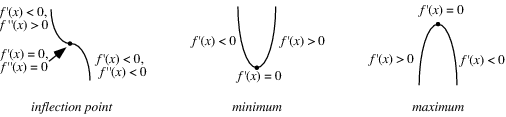
Suppose `f(x)` is continuous at a stationary point `x_0`.
1. If `f^'(x)>`0 on an open interval extending left from `x_0 and f^'(x)<0` on an open interval extending right from `x_0`, then `f(x)` has a local maximum (possibly a global maximum) at `x_0`.
2. If `f^'(x)<0` on an open interval extending left from `x_0 and f^'(x)>0` on an open interval extending right from `x_0, then f(x)` has a local minimum (possibly a global minimum) at `x_0`.
3. If `f^'(x)` has the same sign on an open interval extending left from `x_0` and on an open interval extending right from `x_0, then f(x)` has an inflection point at `x_0`.
Weisstein, Eric W. "First Derivative Test." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/FirstDerivativeTest.html

Second Derivative Test
Suppose `f(x)` is a function of x that is twice differentiable at a stationary point `x_0`.
1. If `f^('')(x_0)>0`, then f has a local minimum at `x_0`.
2. If `f^('')(x_0)<0`, then f has a local maximum at `x_0`.
The extremum test gives slightly more general conditions under which a function with `f^('')(x_0)=0` is a maximum or minimum.
If `f(x,y)` is a two-dimensional function that has a local extremum at a point `(x_0,y_0)` and has continuous partial derivatives at this point, then `f_x(x_0,y_0)=0 and f_y(x_0,y_0)=0`. The second partial derivatives test classifies the point as a local maximum or local minimum.
Define the second derivative test discriminant as
`D = f_(xx)f_(yy)-f_(xy)f_(yx)`
`= f_(xx)f_(yy)-f_(xy)^2`

Then
1. If D>0 and `f_(xx)(x_0,y_0)>0`, the point is a local minimum.
2. If D>0 and `f_(xx)(x_0,y_0)<0`, the point is a local maximum.
3. If D<0, the point is a saddle point.
4. If D=0, higher order tests must be used.
Weisstein, Eric W. "Second Derivative Test." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/SecondDerivativeTest.html

REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 14, 1972.
Thomas, G. B. Jr. and Finney, R. L. "Maxima, Minima, and Saddle Points." §12.8 in Calculus and Analytic Geometry, 8th ed. Reading, MA: Addison-Wesley, pp. 881-891, 1992.