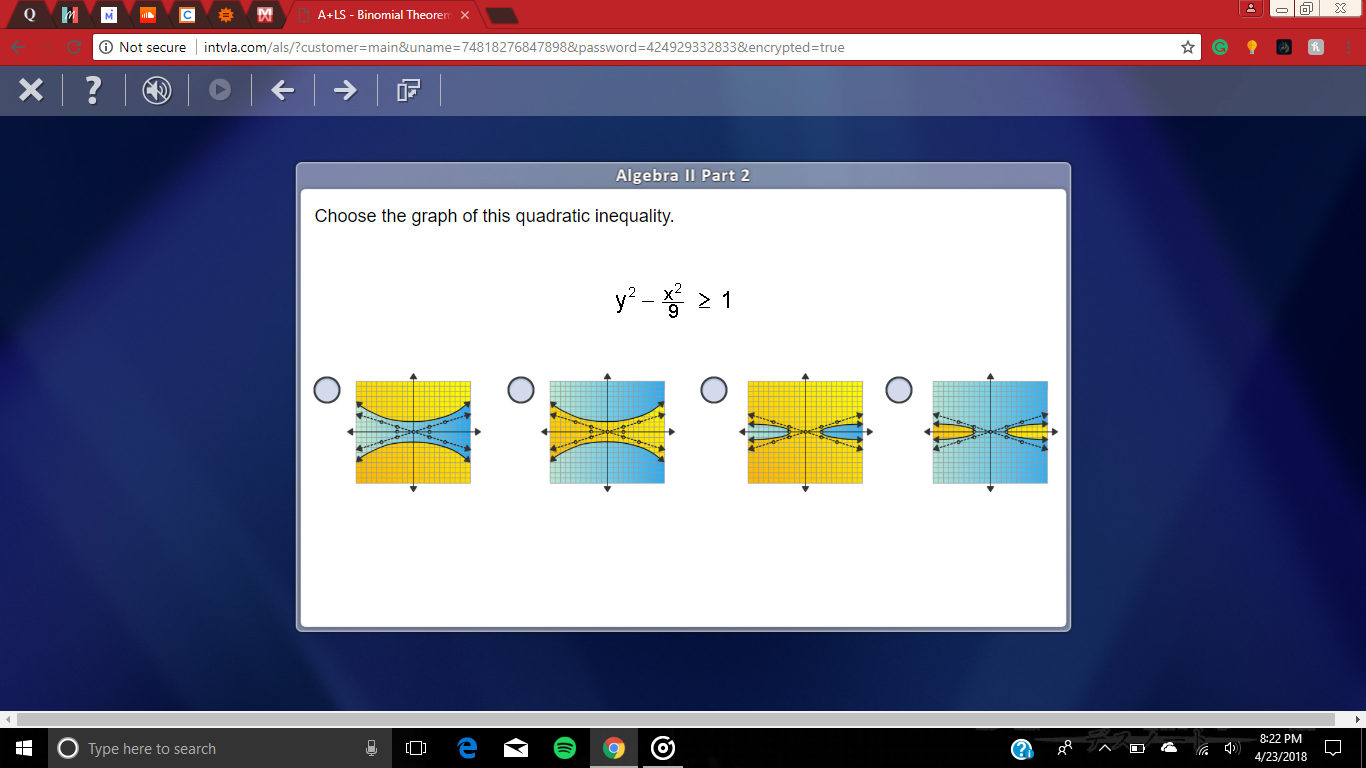
Choose the graph of this quadratic inequality?
1 Answer
The answer is the first graph:
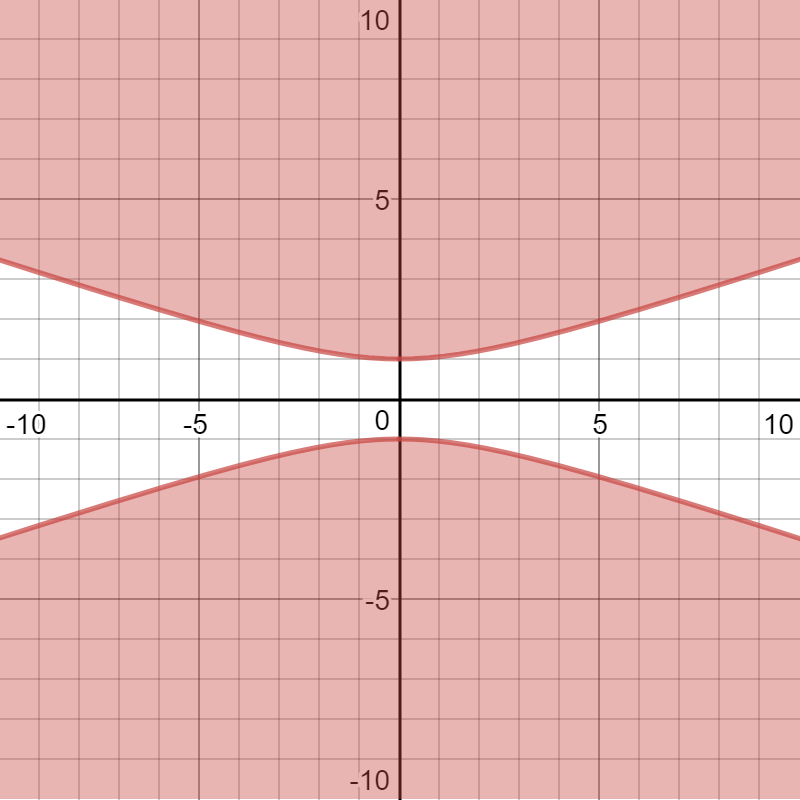
Explanation:
Given
We know that the equation:
Is a hyperbola with a vertical transverse axis; this eliminates graphs 3 and 4 because they have a horizontal transverse axis.
Because the inequality is greater than we choose the graph that has the yellow area above and below the hyperbola; this is graph 1.
Let's pretend that we cannot recognize the equations of a horizontal transverse axis hyperbola or a vertical transverse axis hyperbola and we do not know that the greater than relationship shades in above and below. How do we eliminate the graphs?
We let
Please observe that the points
Please observe that the point
Then it must be graph 1.
