What is the area of an equilateral triangle with sides 8 inches long?
2 Answers
We just apply the formula
Explanation:
Let's derive the formula. The altitude
The area is
Let's check this with my favorite theorem, called Archimedes' Theorem, which, like Heron's formula, relates the area of a triangle to its sides:
Let's plug in
Explanation:
.
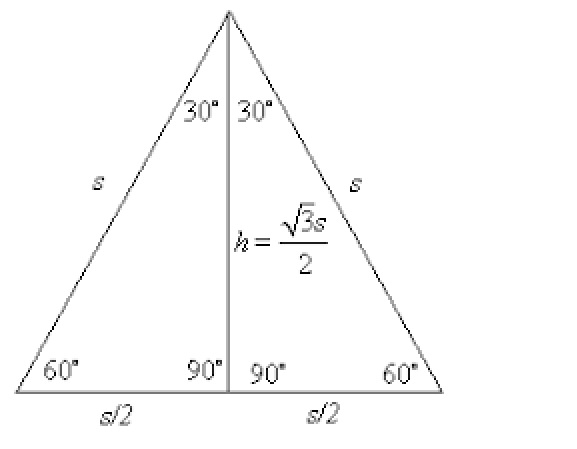
In an equilateral triangle, the altitude divides the base into two equal halves. As shown above, if the measure of the side is
We can use the Pythagorean formula to get the measure of the long leg (altitude):
In our problem,
The formula for the area of a triangle is:


