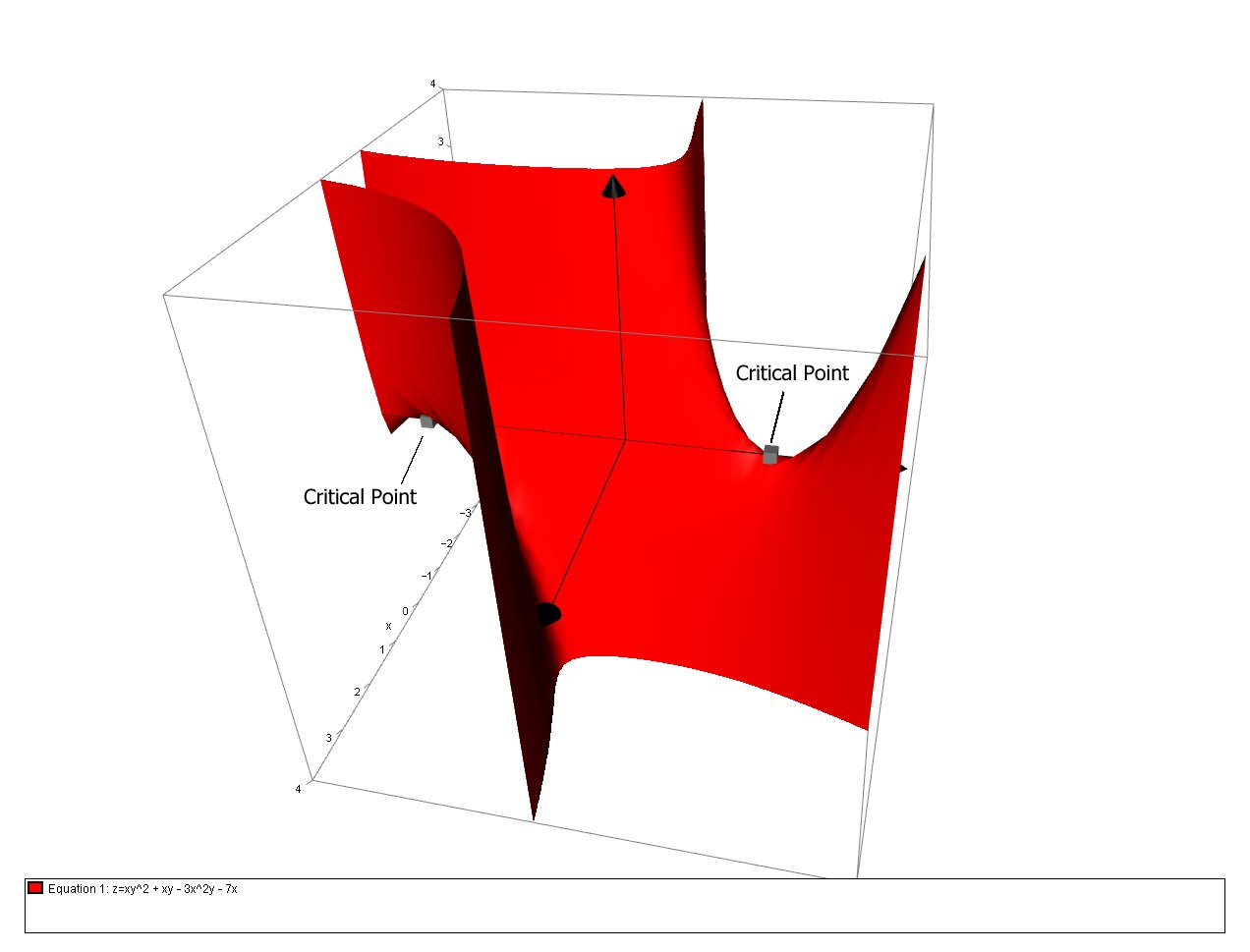
What are the values and types of the critical points, if any, of #f(x, y) = xy^2+xy-3x^2y-7x#?
1 Answer
Saddle points at
Explanation:
We have a 3D surface defined by:
# f(x, y) = xy^2 + xy - 3x^2y - 7x #
Step 1 - Find the Partial Derivatives
We compute the partial derivative of a function of two or more variables by differentiating wrt one variable, whilst the other variables are treated as constant. Thus:
The First Derivatives are:
# f_x \ = (partial f) / (partial x) \ \ = y^2+y-6xy -7 #
# f_y \ = (partial f) / (partial y) \ \ = 2xy+x-3x^2 #
The Second Derivatives are:
# f_(x x) =(partial^2 f) / (partial x^2) = -6y #
# f_(yy) = (partial^2 f) / (partial y^2) = 2x #
The Second Partial Cross-Derivatives are:
# f_(xy) =(partial^2 f) / (partial x partial y) =2y+1-6x #
# f_(yx) = (partial^2 f) / (partial y partial x) =2y+1-6x #
Note that the second partial cross derivatives are identical due to the continuity of
Step 2 - Identify Critical Points
A critical point occurs at a simultaneous solution of
# f_x = f_y = 0 iff (partial f) / (partial x) = (partial f) / (partial y) = 0#
i.e, when:
# y^2+y-6xy -7 = 0# ..... [A]
# 2xy+x-3x^2 = 0# ..... [B]
From [B], we have:
# x(2y+1-3x) = 0 => x=0,1/3(2y+1) #
From [A], we have:
# x=0 => y^2+y -7 = 0 #
# :. y = -1/2+-sqrt(29)/2 #
# x=1/3(2y+1) => y^2+y-6(1/3(2y+1))y -7 = 0 #
# :. y^2+y-4y^2-2y -7 = 0 #
# :. 3y^2+y +7 = 0 # having no real solutions
So we can conclude that there are two critical points:
# (0,-1/2-sqrt(29)/2) # and#(0,-1/2+sqrt(29)/2) #
Step 3 - Classify the critical points
In order to classify the critical points we perform a test similar to that of one variable calculus using the second partial derivatives and the Hessian Matrix.
# Delta = H f(x,y) = | ( f_(x x) \ \ f_(xy) ) , (f_(yx) \ \ f_(yy)) | = | ((partial^2 f) / (partial x^2),(partial^2 f) / (partial x partial y)), ((partial^2 f) / (partial y partial x), (partial^2 f) / (partial y^2)) | = f_(x x)f_(yy)-(f_(xy))^2 #
Then depending upon the value of
# {: (Delta>0, "There is maximum if " f_(x x)<0),(, "and a minimum if " f_(x x)>0), (Delta<0, "there is a saddle point"), (Delta=0, "Further analysis is necessary") :} #
Using custom excel macros the function values along with the partial derivative values are computed as follows:
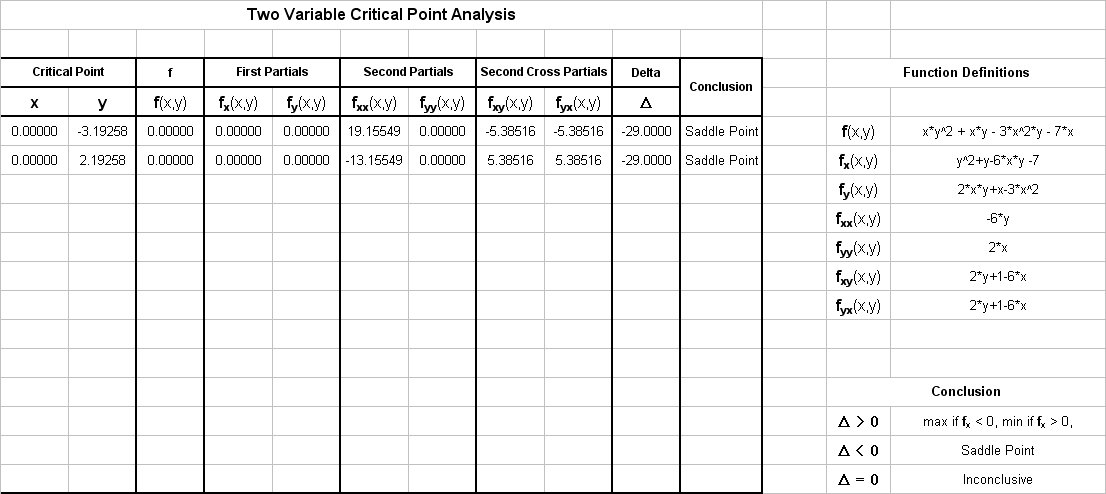
And we can confirm these results graphically