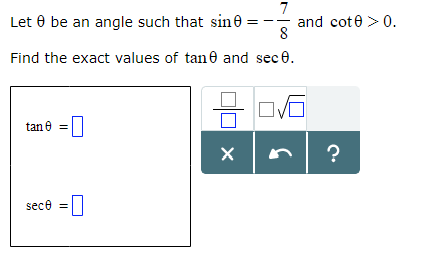
We're told that sintheta is negative; however, cottheta=costheta/sintheta is positive.
This tells us that both sine and cosine must be negative (the negatives cancel out to give a positive cotangent), so we're working in the fourth quadrant.
Then, tantheta=sintheta/costheta will also be positive.
Furthermore, since sectheta=1/costheta, sectheta will also be negative as a result of the negative cosine.
Keeping this in mind, we'll continue.
Recall the identity
sin^2theta+cos^2theta=1
sintheta=(-7/8), sin^2theta=(-7/8)^2=49/64
Thus,
49/64+cos^2theta=64/64
cos^2theta=(64-49)/64
cos^2theta=15/64
costheta=+-sqrt(15/64)=+-sqrt15/8
We want the negative result:
costheta=-sqrt15/8
Then,
sectheta=1/costheta=1/(sqrt15/8)=-8/sqrt15
Rationalizing the denominator (multiply by sqrt15/sqrt15), we get
sectheta=-(8sqrt15)/15
We can now find the tangent:
tantheta=sintheta/costheta
tantheta=(cancel-7/8)/(cancel-(8sqrt15)/15)
tantheta=7/8*15/(8sqrt15)
tantheta=105/(64sqrt15)
Rationalizing, we get
tantheta=(105sqrt15)/(960)
tantheta=(7sqrt15)/(64)