Help please? Compared to the graph of the function #f(x) = sqrtx#, how is the graph of #g(x)= sqrt(x+8)-4# translated?
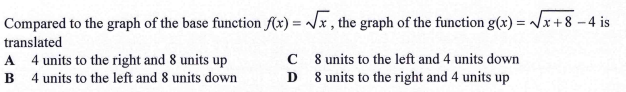
2 Answers
C
Explanation:
It has been shifted down
Here, the function is being horizontally shifted 8 units left
Here, the function is being vertically shifted 4 units down
Explanation:
It's confusing, but I just think of
Let's just pop this into Socratic's grapher and make sure.
graph{sqrt(x+8) -4 [-8.71, 11.29, -5.12, 4.88]}


