Question

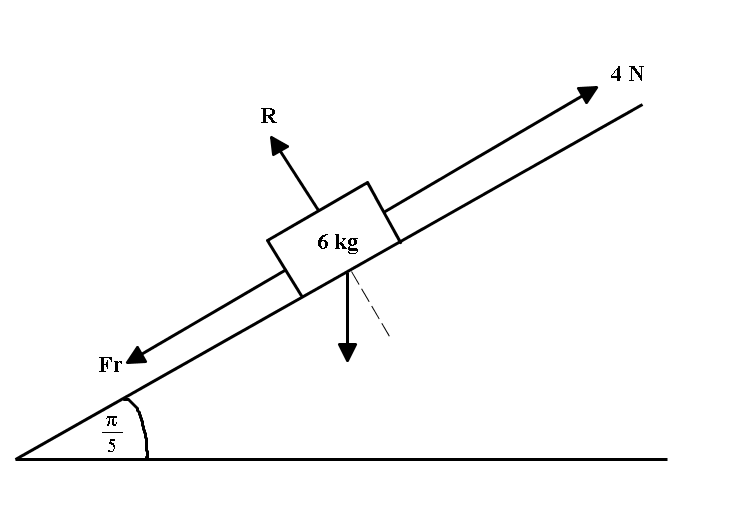
An body with a mass of `6 kg` is on a slope at an incline of `pi/5`. If the body is being pushed up the slope with a force of `4 N`, what is the minimum coefficient of friction required for the body to remain at rest?

I have got `0.643 N`, but I don.t think this is correct.

Answer 1

`mu = {m.g sin (pi/5) -4 } / {mg. cos (pi/5)} =0.65`

Explanation:

the body on the incline will have forces -

1. the weight mass.g acting vertically downwards

2. the force of 4 N pushing it up the incline

3. the force of normal reaction perpendicular to the incline R

4. the force of friction F(r) acting along the incline with direction opposite to the tendency of movement of the body.

the weight of the body can be resolved in two components one perpendicular to the incline `=`m.g.`cos (pi/5)`

and another along the incline `= mg sin(pi/5)`
as the angle between vertical and perpendicular to the incline is same as the angle of incline with horizontal.

as the pushing force of 4 N is smaller than `mg sin(pi/5)` therefore the body will have tendency to slide down the slope.

and if it is not sliding i.e. balanced by force of friction acting up along the slope
therefore

`mg.sin(pi/5) = 4 + mu. mg cos(pi/5)`
or

`mu = {m.g sin (pi/5) -4 } / {mg. cos (pi/5)}`

taking `m=6 kg , g= 9.8 m/s^2 ; Sin(pi/5) = 0.588`
and `cos (pi/5) = 0. 801` (from table of sine and cosines)

`mu = ( ( 6 ).( 9.8) .(0.588) -4 ) / (6 * 9.8 (0.801)`

`mu = 0.65`