.There was a proposal for the new size of the advisory boards to be placed at strategic locations along the expressway. The board must contain 50 square meters of print and margins of 4 meters at the top and bottom while 3 meters on each side.?

a. Find a mathematical model expressing the total area of the board as a function of the horizontal dimension of the region covered by the printed material.
b. Determine the domain of the function.
c. Prove that the function is continuous on its domain.
d. Sketch the graph of the function obtained in (a).
e. Determine (to the nearest meter) the dimensions of the smallest board that meets the specifications.

1 Answer
Steve M
Apr 30, 2018

To the nearest #m#, the sought dimensions are: #12 \ m xx 16 \ m#

Explanation:

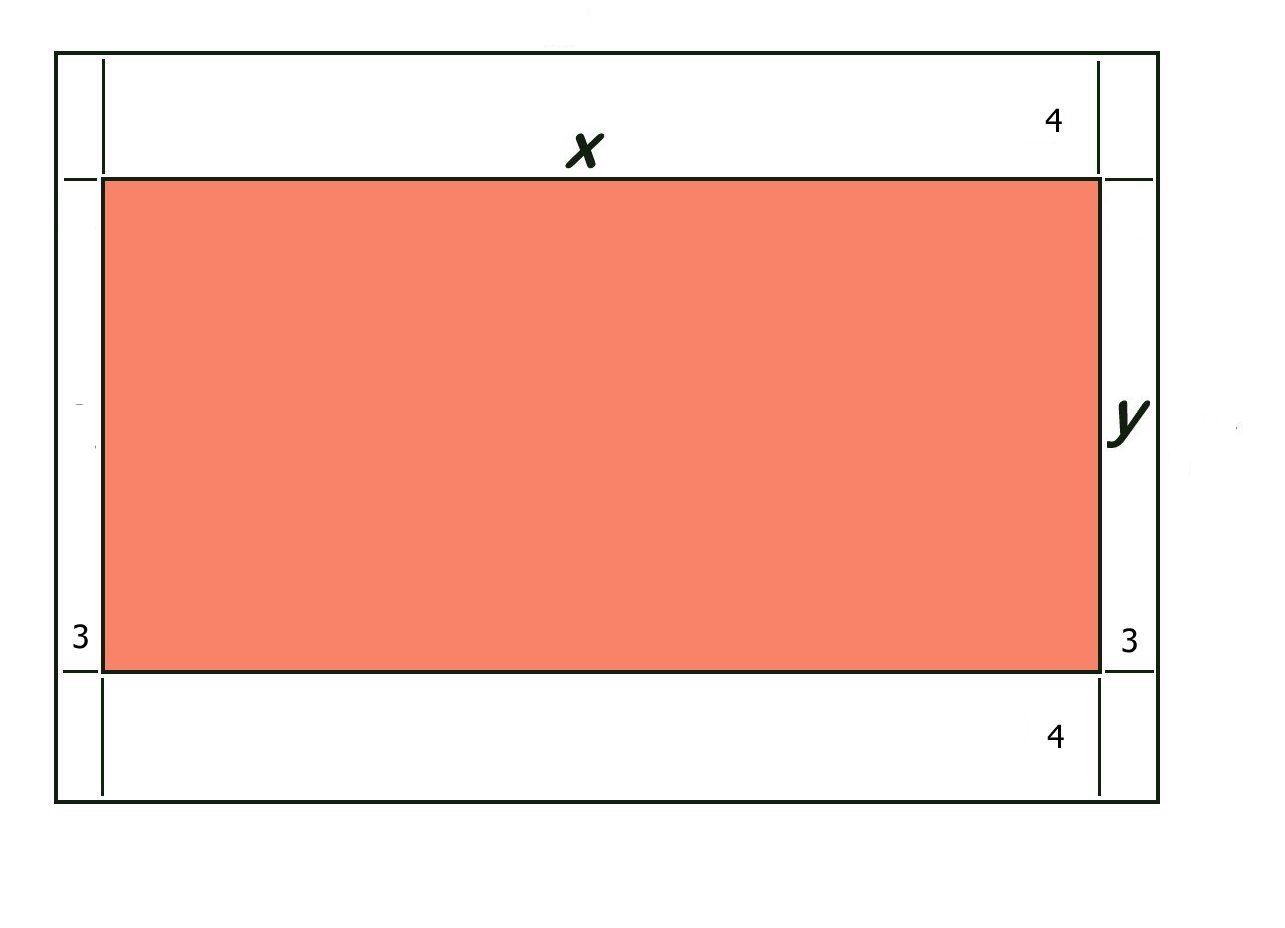
enter image source here

Let us set up the following variables:

# {(x, "Printed width of poster (m)"), (y, "Printed height of poster (m)"), (A, "Total Area of the board (m"^2")") :} #

Part (A):

Then the dimensions of the entire board are:

# {("Width", =x+3+3,=x+6), ("Height", =y+4+4,=y+8) :} #

And so the total Area of the board is given by:

# A=(x+6)(y+8) #

But we also know that the print area is #50 \ m^2#, so that:

# xy = 50 => y=50/x#

Thus by substitution into the earlier result, we have:

# A = (x+6)(50/x+8) #

# \ \ \ = x(50/x+8) + 6(50/x+8)#

# \ \ \ = 50+8x+300/x + 48 #

# \ \ \ = 8x+300/x + 98 #

Part (B):

The function is defined for all values #x# with the exception of a discontinuity at #x=0#. So the domain of the function is:

# { x in RR | x != 0 } #

Given the context of the problem, we cannot have a negative length, so in reality we have a domain:

# { x in RR | x gt 0 } => x in (0,oo)#

Part (C):

An Intuitive "proof": The function is defined for all values #x# with the exception of a discontinuity at #x=0#. Hence, given the restricted domain #x in (0,oo)# the function is well defined and behaved, and thus it is continuous.

Part (D):

graph{y=8x+300/x + 98 [-5, 30, -50, 500]}

Part (E):

For maximum or minimum, we seek a critical point of the area function, #A(x)# wet #x#. We therefore consider its derivative:

# f'(x) = 8 -300/x^2 #

At a critical point, the first derivative vanishes, thus we require:

# f'(x) = 0 => 8 -300/x^2 = 0 #

# :. 300/x^2 = 8 #

# :. x^2 = 300/8 #

# :. x = +-sqrt(300/8) = +- (5sqrt(6))/2 #

We discard the negative solution (due to the domain restriction), thus we gain a single solution

# x = (5sqrt(6))/2 ~~ 6.1 \ m#

Which gives us:

# A(x) = 8*(5sqrt(6))/2 + 300/((5sqrt(6))/2) + 98 #

# \ \ \ \ \ \ \ \ = 20sqrt(6)+20sqrt(6)+98 #

# \ \ \ \ \ \ \ \ = 98 + 40sqrt(6) \ m^2#

# \ \ \ \ \ \ \ \ ~~ 196.0 \ m^2#

We can visually confirm from the graph, that the solution is both consistent and corresponds to a minimum, and the dimensions of the board sought are thus:

# {("Width", =(5sqrt(6))/2+6, ~~ 12.12 \ m), ("Height", =(50*2)/(5sqrt(6))+8, ~~ 16.16 \ m) :} #

Related questions
Impact of this question
492 views around the world
You can reuse this answer
Creative Commons License