Question

What is the expected value of the sum of two rolls of a six sided die?

Answer 1

`7`

Explanation:

Intuitively we would expect the sum of a single die to be the average of the possible outcomes, ie:

`S= (1+2+3+4+5+6)/6 = 3.5`

And so we would predict the sum of a two die to be twice that of one die, ie we would predict the expected value to be `7`

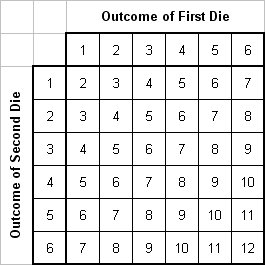
If we consider the possible outcomes from the throw of two dice:

And so if we define `X` as a random variable denoting the sum of the two dices, then we get the following distribution:

So then we compute the expected value, using

`E(X) = sum x(P(X)=x)`

`\ \ \ \ \ \ \ \ \ = 2 * 1/36 + 3 * 2/36 + 4 * 3/36 + 5 * 4/36`
`\ \ \ \ \ \ \ \ \ \ \ \ \ + 6 * 5/36 + 7 * 6/36 + 8 * 5/36 + 9 * 4/36`
`\ \ \ \ \ \ \ \ \ \ \ \ \ + 10 * 3/36 + 11 * 2/36 + 12 * 1/36`

`\ \ \ \ \ \ \ \ \ = (2+6+12+20+30+42+40+36+30+22+12)/36`

`\ \ \ \ \ \ \ \ \ = (252)/36`

`\ \ \ \ \ \ \ \ \ = 7`