Change the order of integration and evaluate?

Question

9669 views around the world

You can reuse this answer
Creative Commons License

Answer 1 · 2018-05-01T08:15:33

Below

If you do change you need to split the integration out as:

#int_0^1 \ int_0^sqrty \ xy \ dx \ dy + int_1^2 \ int_0^(2 - y)\ xy \ dx \ dy#

#= int_0^1 \ (1/2x^2y)_0^sqrty \ dy + int_1^2 \ (1/2x^2y)_0^(2 - y) \ dy#

#=1/2 int_0^1 \ y^2 \ dy + 1/2int_1^2 \ 4y -4y^2 + y^3 \ dy#

#=1/2 ( (y^3/3)_0^1 + (\ 2y^2 -4/3 y^3 + y^4/4 )_1^2) = 3/8 #

Whereas:

#int_0^1 \ int_(x^2)^(2-x) \ xy \ dy\ dx#

#= int_0^1 \ ( 1/2 xy^2 )_(x^2)^(2-x)\ dx#

#=1/2 int_0^1 \ 4x - 4x^2 + x^3 - x^5 \ dx#

#=1/2 (2x^2- 4/3 x^3 + x^4/4 - x^6/6)_0^1 = 3/8#

Answer 2 · 2018-05-01T14:31:48

To change the order of integration, please see below.

The region over which we are integrating is bounded by #y = x^2# and #y = 2-x# from #x=0# to #x = 1#

Here is the region:

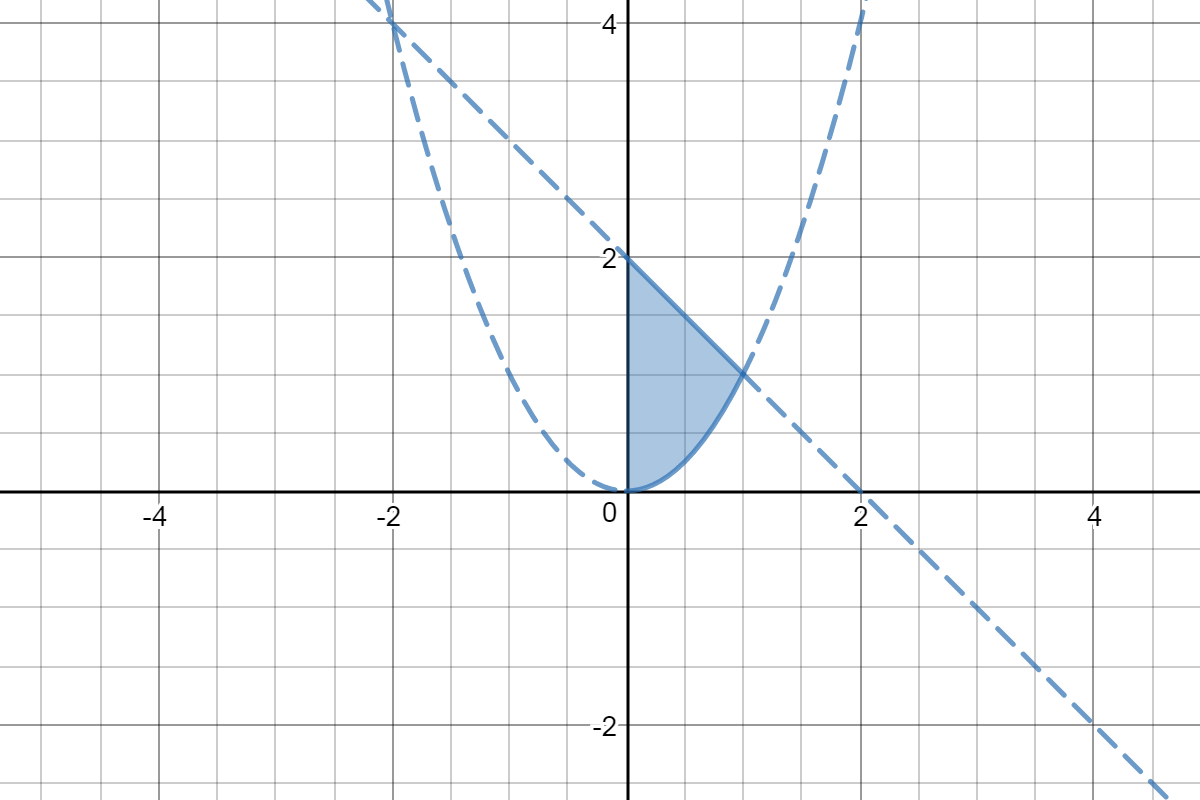
enter image source here

To change the order of integration, we need to re-describe the region.

Apparently #y# goes from #0# to #2# and the region is split into two parts.

From #y=0# to #y=1#, the bounds are #x=sqrty# (solve #y = x^2# for #y# in the first quadrant) and #x = 0#

From #y=1# to #y=2#, the bounds are #x=2-y# (solve #y = 2-x# for #y#) and #x = 0#

The function to be integrated is #f(x,y) = xy# so we have

#int_0^1 int_0^(sqrty) xy\ dx\ dy + int_1^2 int_0^(2-y) xy\ dx\ dy#

Please see the other answer for evaluation.