Question

What are all actual roots of `P(x) = x^3 - 3x^2 + 4x - 12`?

Answer 1

`x = 3`

Explanation:

`0 = x^3 - 3x^2 + 4x - 12`

`0 = x^2(x-3) + 4(x-3)`

`0 = (x^2+4)(x-3)`

`0 = x^2 + 4` and `0 = x-3`

`-4 = x^2quad` and `quad3 = x`

We know that we can't square root a negative number, so `-4 = x^2` cannot be a solution.

Therefore, our only solution is `3`. The root is `3`.

To prove this, let's graph this:

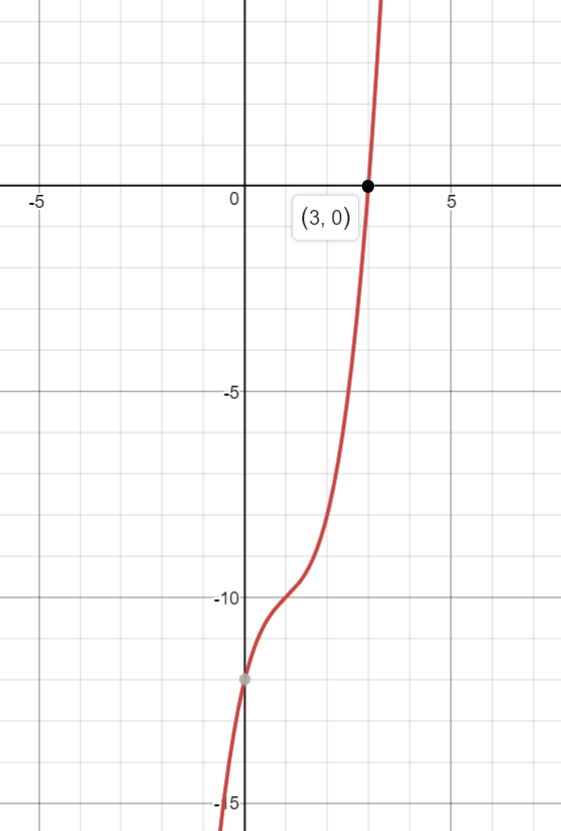
(desmos.com)

As you can see, the only zero or root of the equation is at `(3, 0)`, meaning that our solution is correct.

Hope this helps!