Given the equation in picture below, what is? : a. f'(x) b. the derivative of e^(f(x))
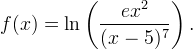
1 Answer
(a)
f'(x) = -(5x+10)/(x(x-5)) (b)
d/dxe^f(x) = - (5ex( 2+x)) / (x-5)^8
Explanation:
We seek (a)
f(x) = ln ((ex^2)/(x-5)^7)
Part (a):
Using the properties of logarithms, we can write:
f(x) = ln (e) + ln (x^2) - ln(x-5)^7
\ \ \ \ \ \ \ = 1 +2lnx-7ln(x-5)
So, we can differentiate to get:
f'(x) = 0 +2/x -7/(x-5)
\ \ \ \ \ \ \ \ = (2(x-5)-7x)/(x(x-5))
\ \ \ \ \ \ \ \ = (2x-10-7x)/(x(x-5))
\ \ \ \ \ \ \ \ = -(5x+10)/(x(x-5))
Part (b):
Let:
g(x) = e^(f(x))
Then:
g(x) = e^(ln ((ex^2)/(x-5)^7))
\ \ \ \ \ \ \ = (ex^2)/(x-5)^7
And using the quotient rule (and chain rule), we have:
g'(x) = { ((x-5)^7)(2ex) - (7(x-5)^6)(ex^2) } / ((x-5)^7)^2
\ \ \ \ \ \ \ \ = { 2ex(x-5) - 7ex^2 } / (x-5)^8
\ \ \ \ \ \ \ \ = { 2ex^2-10ex - 7ex^2 } / (x-5)^8
\ \ \ \ \ \ \ \ = { -10ex - 5ex^2 } / (x-5)^8
\ \ \ \ \ \ \ \ = - (5ex( 2+x)) / (x-5)^8

