.
The bucket has a base diameter of #12# and top opening diameter of #20#. This makes the base radius #6# and top radius #10#.
Let's look at the figure below:
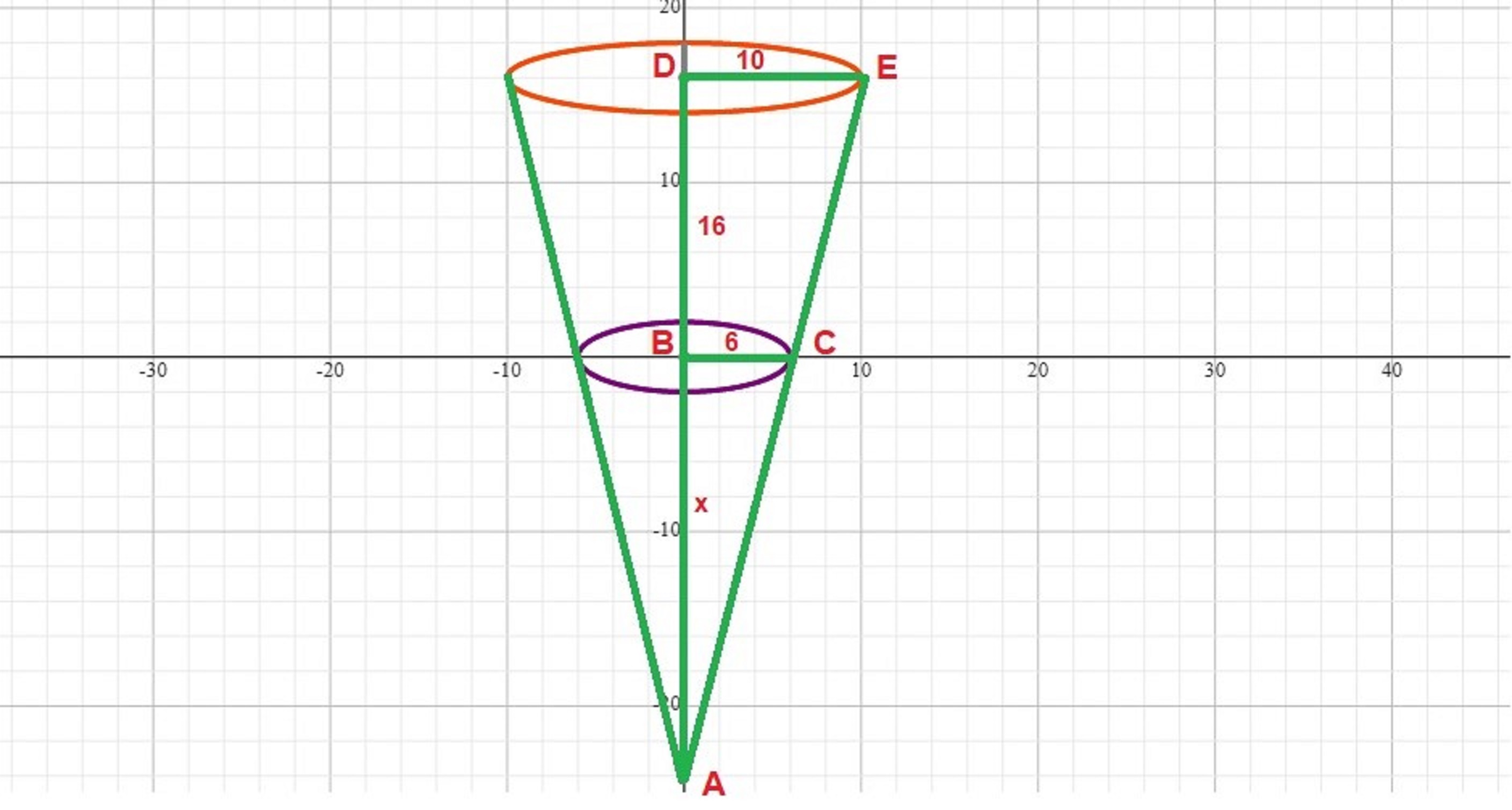
The bucket as shown has the bottom base of radius:
#BC=6#
and the top opening of radius:
#DE=10#
The depth is:
#DB=16#
If we extend the lateral surface of the bucket down it will generate a cone that contains the bucket in it.
To calculate the volume of the bucket, we need to calculate the volume of the large cone with the depth of #DA#, then calculate the volume of the small cone with the depth of #BA#, and subtract the volume of the small cone from the volume of the large cone.
Let's let #BA=x#. The two triangles #DeltaABC# and #DeltaADE# are similar due to the Angle Angle theorem because they both share angle #/_ADE=90^@# and angle #/_DAE#.
Therefore, the ratio of their corresponding sides are equal.
#(BA)/(DA)=(BC)/(DE)#
#x/(16+x)=6/10#
#x/(16+x)=3/5#
#48+3x=5x#
#2x=48#
#x=24# cm
The volume of a cone is:
#V=1/3hpir^2#
The height #(h)#, which we are calling the depth, of the small cone is #x=24 cm# and the depth of the large cone is #x+16=24+16=40 cm#
#V_("Large Cone")=1/3(40)(pi)(10)^2=(4000pi)/3cm^3#
#V_("Small Cone")=1/3(24)(pi)(6)^2=288picm^3#
#V_("Bucket")=(4000pi)/3-288pi=(3136pi)/3cm^3#
Volume of a cylinder is:
#V_("Cylinder")=pir^2h# where #h# is the height(depth) and #r# is the radius of the base of the cylinder.
If the base of the cylinder has a diameter of #28cm# then the radius of the base is #14cm#
#(pi)(14)^2(h)=(3136pi)/3#
#196pih=(3136pi)/3#
#196h=3136/3#
#h=(3136/3)/196=3136/588=5.33cm#


