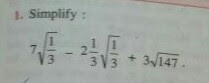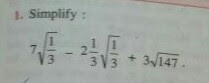We will use the fact that sqrt(a/b)=sqrta/sqrtb
7*sqrt1/sqrt3-7/3*sqrt1/sqrt3+3sqrt147
=7/sqrt3-7/(3sqrt3)+3sqrt147
=(7sqrt3)/3-(7sqrt3)/9+3sqrt147
=(21sqrt3)/9-(7sqrt3)/9+3sqrt147
=(14sqrt3)/9+3sqrt147
I've left the 3sqrt147 up till now, cos its nasty to deal with. However, seeing that we have an expression with sqrt3, there's a good chance that 147 will be equal to three times a square number. Some good ol' bus shelter long division (or using a calculator if you're allowed) will show you that 147=3xx49 Since 49 is a square number, we can work on simplifying this more
=(14sqrt3)/9+3[sqrt(3xx49)]
=(14sqrt3)/9+3(7sqrt3)
=(14sqrt3)/9+21sqrt3
=(14sqrt3)/9+(189sqrt3)/9
=203/9sqrt3