Why the gratuitous #pi#?
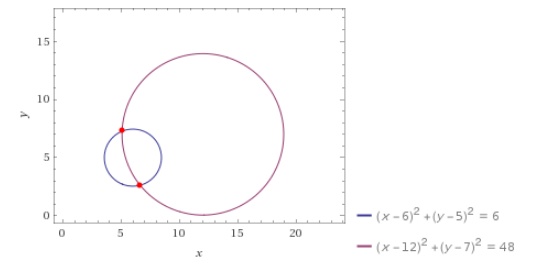
The area is #A =pi r^2# so #r^2=A/pi.# So the first circle has a radius #r_1=\sqrt{6}# and the second #r_2=sqrt{48}=4 sqrt{3}#.
The centers are #sqrt{(12-6)^2+(7-5)^2}= sqrt{40} = 2 sqrt{10}# apart.
So the circles overlap if #sqrt{6} + 4 sqrt{3} ge 2 sqrt{10} #.
That's so ugly that you'd be forgiven for reaching for the calculator. But it's really not necessary. Let's take a detour and look how this is done using Rational Trigonometry. There we're only concerned with the squared lengths, called quadrances.
Let's say we want to test if three quadrances #A,B,C# are the quadrances between three collinear points, i.e. #sqrt{A}=sqrt{B}+sqrt{C}# or #sqrt{B}=sqrt{A}+sqrt{C},# or #sqrt{C}=sqrt{A}+sqrt{B}#. We'll write it as
# pm sqrt{C} = pm sqrt{A} pm sqrt{B}#
Squaring,
#C = A + B \pm 2 sqrt{AB}#
#C - A-B = pm 2 sqrt{AB}#
Squaring again,
#(C-A-B)^2 = 4AB #
#0 = 4AB - (C-A-B)^2 #
It turns out
#mathcal{A} = 4AB - (C-A-B)^2 #
is a discriminant for triangles. We just showed if #mathcal{A} =0# that means we have a degenerate triangle, formed from three collinear points. If #mathcal{A} > 0# then we have a real triangle, each side less than the sum of the other two. If #mathcal{A}<0# we don't have sides that satisfies the triangle inequality, and we sometimes call this an imaginary triangle.
Let's turn back to our question armed with our new triangle discriminant #mathcal{A}#. If the circles intersect we we can make a triangle of the two centers and an intersection, so the sides will have lengths #r_1#, #r_2#, and the distance between the centers #(6,5)# and #(12,7)#. We have
# A = r_1^2 = 6#
#B = r_2^2 = 48 #
#C= (12-6)^2+(7-5)^2=40#
#mathcal{A} = 4AB - (C-A-B)^2 = 4(6)(48) - (40 - 6 - 48)^2 = 956 #
#mathcal{A} > 0# so we have a real triangle, i.e overlapping circles.
Oh yeah, for any triangle #mathcal{A} = 16 (text{area})^2 .#
Check: Alpha