Question

What is the perimeter of a triangle with vertices of (2,0), (2, -3) and (-2,-3)?

Answer 1

The perimeter is 12.

Explanation:

The best way to start on this question is to plot those points and draw the triangle.

You can immediately see that it is a right triangle.

You can count the intervals between (2,0) and (2,-3).

Then you can count the intervals between (2,-3) and (-2,-3)

Now you can see that it is a 3-4-5 right triangle.

Therefore, with no work at all, you know that the perimeter is 12.
`color(white)(mmmmmmm)`__

To solve this problem with math instead of counting:

1) Find the length of one leg
The distance between (2,0) and (2,-3) is
0 - (-3), which is 3

2) Find the length of the other leg
The distance between (2,-3) and (-2,-3) is
2 - (-2), which is 4.

3) A right triangle with legs 3 and 4 must be a 3-4-5 right triangle.

4) So the perimeter (the sum of the lengths of all three sides) must be
3 + 4 + 5, which is 12.

Answer:
The perimeter is 12.

Answer 2

`" "`
Perimeter of the triangle = 12 units.

Explanation:

`" "`
`"Given Vertices: "color(red)( A(2,0), B(2,-3) and C(-2,-3)`

`color(green)("Step 1:"`

Construct a triangle ABC with the given vertices:

`color(green)("Step 2:"`

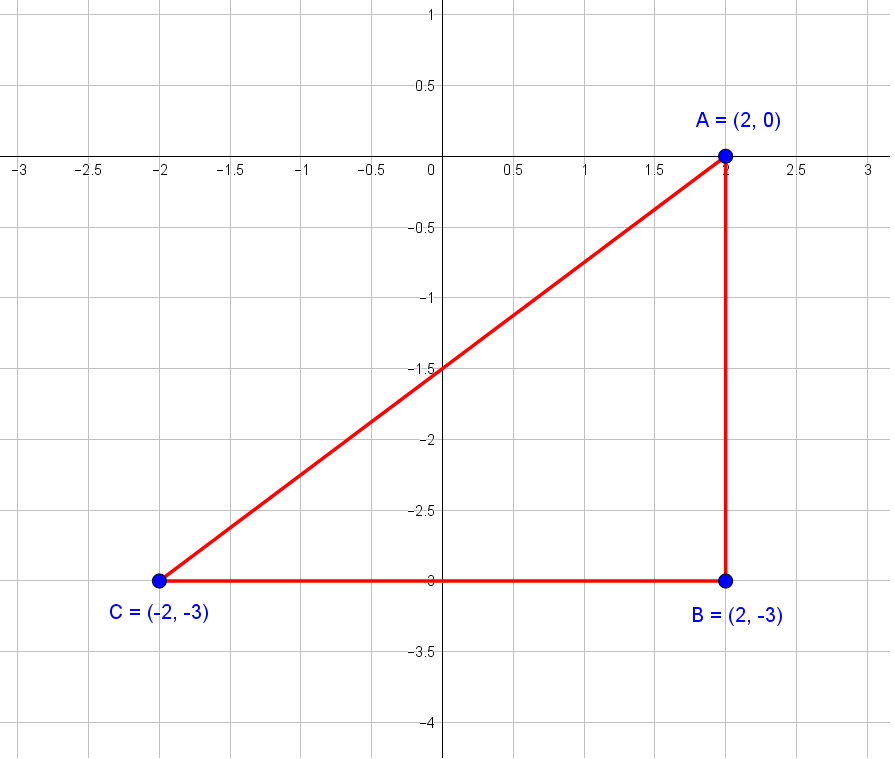
Perimeter of the triangle ABC : `color(blue)(bar(AB)+bar(BC)+bar(AC)`

`bar(AB) " refers to the distance between the two points A and B"`.

To find the magnitudes of the sides AB, BC and AC, use the distance formula:

`"Distance between two points " = color(red)(sqrt((x_2-x_1)^2+(y_2-y_1)^2)`

`color(green)("Step 3:"`

Distance(D) between the two points: `color(brown)(A(2,0) and B(2,-3)`

`D = bar(AB) = sqrt((2-2)^2+(-3-0)^2)`

`rArr sqrt(9)`

`rArr 3`

`"Distance between the Points A and B: 3 Units"`

`color(green)("Step 4:"`

Distance between two points: `color(brown)(B(2,-3) and c(-2,-3)`

`D =bar(BC) = sqrt((-2-2)^2+(-3-(-3)^2)`

`rArr sqrt((-4)^2)`

`rArr sqrt(16`

`rArr 5`

`"Distance between the Points B and C: 4 Units"`

`color(green)("Step 5:"`

Distance between two points: `color(brown)(A(2,0) and C(-2,-3)`

`D = bar(AC)=sqrt((-2-2)^2+(-3-0)^2)`

`rArr sqrt((-4)^2+(-3)^2)`

`rArr sqrt(16+9`

`rArr sqrt(25)`

`rArr 5`

`"Distance between the Points A and C: 5 Units"`

`color(green)("Step 6:"`

Hence, the Perimeter of the triangle ABC

`=3+4+5=12 " Units"`

`color(green)("Step 7:"`

Measure the distances between points on the coordinate plane:

`color(green)("Step 8:"` Useful information

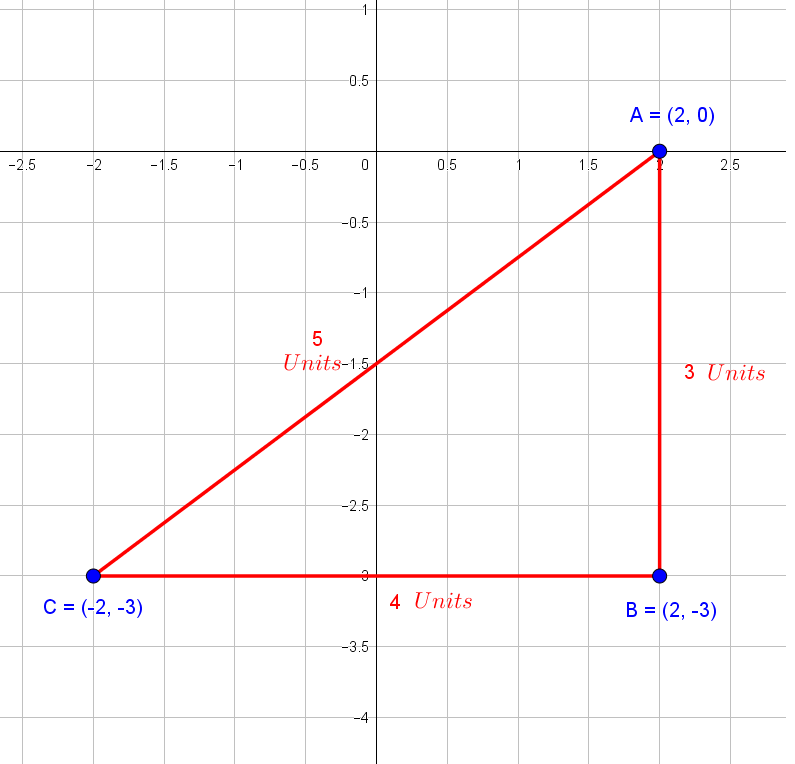
Measure the angle `/_ ABC`

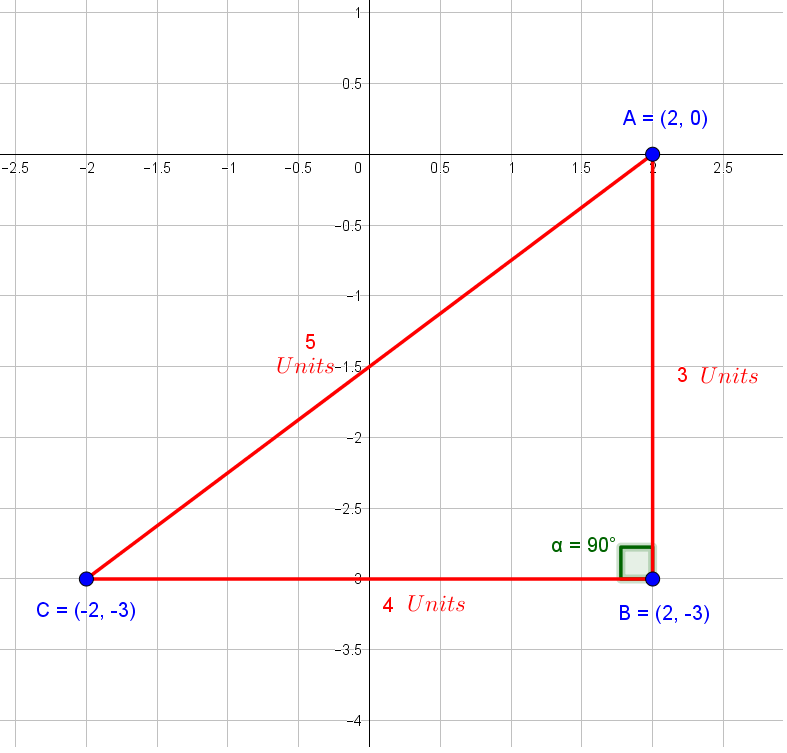
Verify that the angle is `90^@`

Hence, triangle `ABC` is a right-triangle.

Hope it helps.