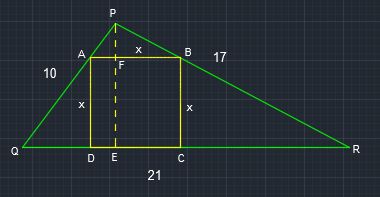
If three sides of a triangle are known, we can use Heron's formula to find the area of the triangle,
#A=sqrt(s(s-a)(s-b)(s-c))#,
where #s=(a+b+c)/2, and a,b, and c# are the lengths of the sides of the triangle.
Let #|PQR|# be area of #DeltaPQR#,
given #PQ=10, PR=17, and QR=21#,
#s=(10+17+21)/2=24#
#=> |PQR|=sqrt(24(24-10)(24-17)(24-21))=sqrt(24*14*7*3)=84 " units"^2#
#|PQR|=1/2*QR*PE=1/2*21*PE=84#,
#=> PE=(84xx2)/21=8# units
let #AB=AD=x, => FE=x#
#=> PF=PE-FE=8-x#
#DeltaPAB and DeltaPQR# are similar,
#=> (PF)/(AB)=(PE)/(QR)#,
#=> (8-x)/x=8/21#
#=> 29x=168, => x=168/29# units,
Hence, perimeter of square #ABCD=4x=4*168/29~~23.2# units

