Can someone solve this? :)
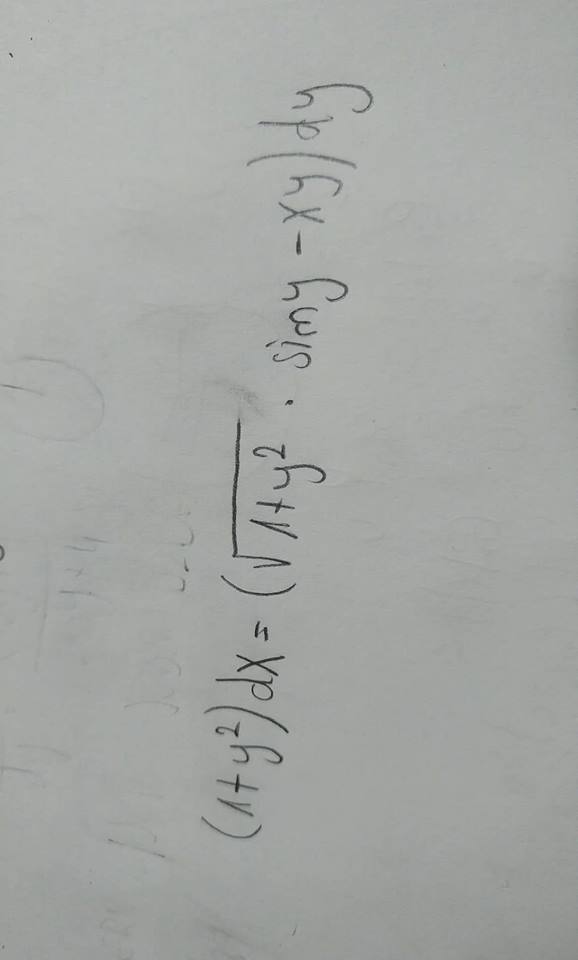
1 Answer
This is a first order linear differential equation
Explanation:
Start off by rearranging the equation. Get the
In this question we rearrange the equation by getting
-> This is a linear differential equation of the type
(Here P and Q are functions of y)
In this equation
The integrating factor for the equation is :
->
->
->Solving the integral using substitution
-> Let
->Upon differentiating , you get ,
You end up with
Integrating factor is ->
Multiplying this factor on both sides and then integrating ,
->
Cancelling
Upon integrating ,
Therefore the final answer is :
->

