Diagrams are great for this stuff!
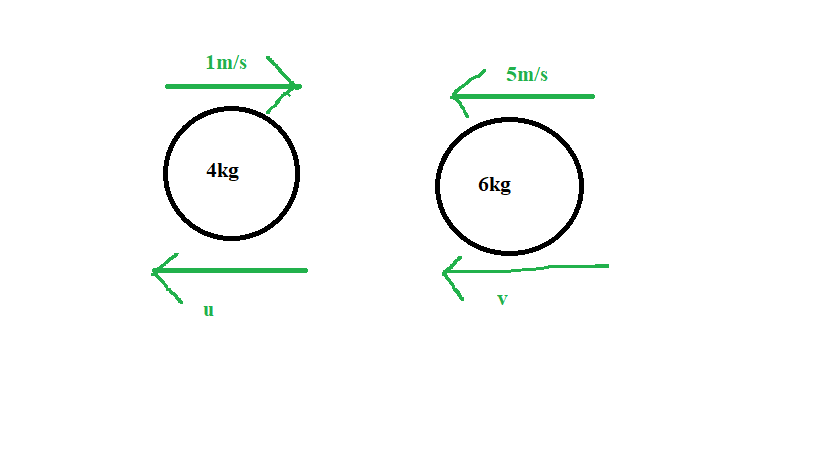
Let the #4kg# ball have a final velocity of #u#, and the #6kg# have a final velocity of #v#
I'm gonna change the question slightly, in that I'll take the second ball to have #5"m/s"# and the first to have #-1"m/s"#. The maths is exactly the same, but since the balls will probably rebound in the same direction as the 6kg one is travelling, this stops having loads of negatives everywhere.
#"KE before"=1/2xx4xx(-1)^2+1/2xx6xx5^2#
#=77J#
#"KE after"=77xx0.9#
#=69.3J#
#:.69.3=1/2xx4xxu^2+1/2xx6xxv^2#
#69.3=2u^2+3v^2" " (1)#
We can form another equation using the conservation of momentum, and solve simultaneously.
#"Using conservation of momentum"#
#"momentum before"="momentum after"#
#4xx(-1)+6xx5=4u+6v#
#26=4u+6v#
#13=2u+3v#
#2u=13-3v#
#u=13/2-3/2v#
#"sub in eqn" (1)#
#69.3=2(13/2-3/2v)^2+3v^2#
#69.3=2(169/4-39/2v+9/4v^2)+3v^2#
#69.3=169/2-39v+9/2v^2+3v^2#
#15/2v^2-39v+76/5=0#
#75v^2-390v+152=0#
From the quadratic formula:
#v=(390+-sqrt(390^2-4xx75xx152))/(2xx75#
#v=4.78# or #v=0.424#
#u=13/2-3/2v#
Let #v=4.78#
#u=13/2-3/2(4.78)#
#u=-0.67#
However, since the #6kg# particle is in the same direction as its original motion (v is positive and we decided its initial velocity was +5m/s), the direction of motion of the #4kg# particle should also be reversed. So we reject this pair of values.
Let #v=0.424#
#u=13/2-3/2(0.424)#
#=5.864#
So the speed of the 4kg particle is 5.86 m/s, and the speed of the 6kg particle was 0.424 m/s. Since they are travelling, in the context given by the question (we reversed this for our maths, remember?), their final speeds are #-5.86" m/s"# and #-0.424" m/s"# respectively.

