Question

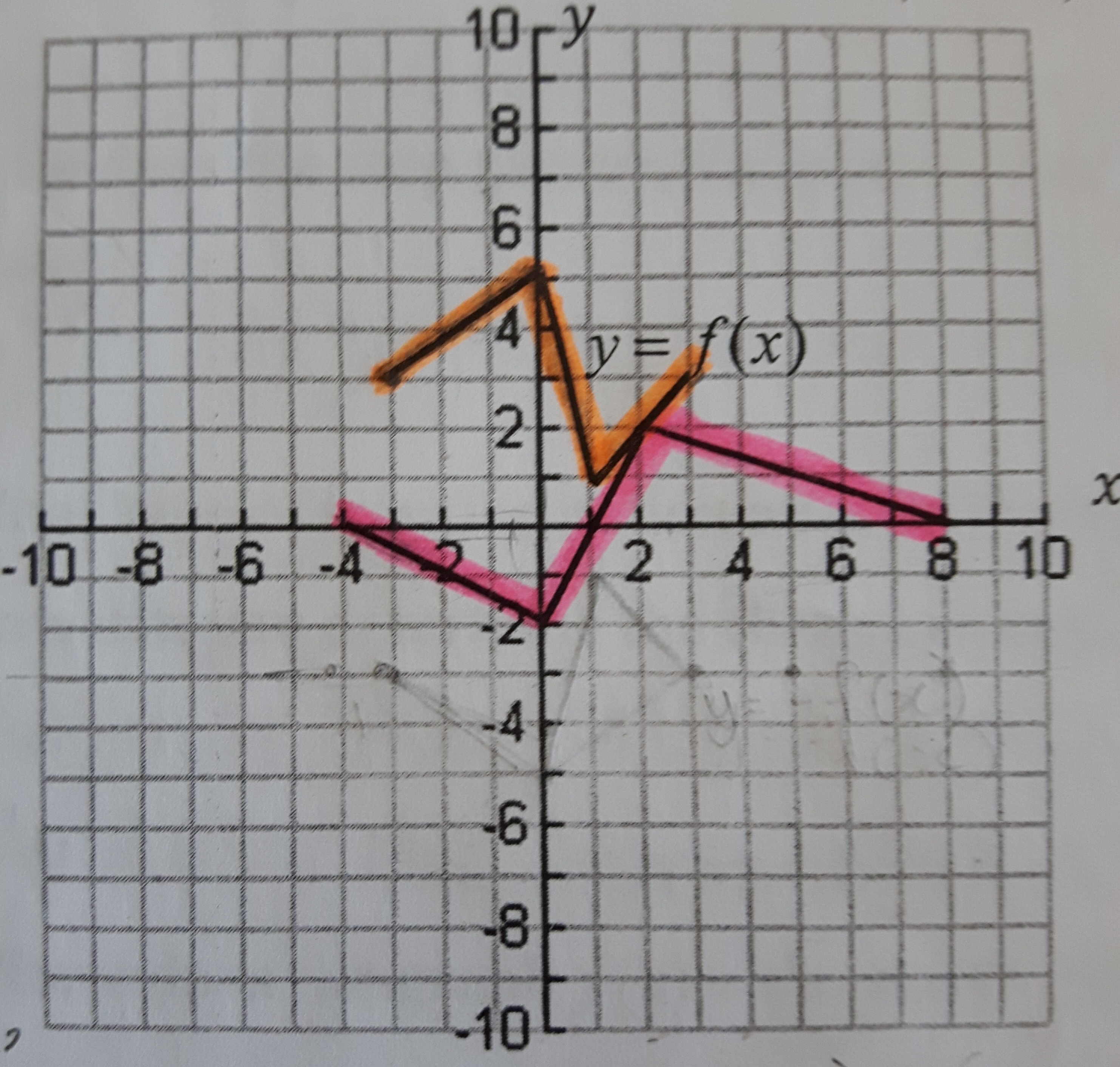
The orange graph is the function f(x). How do you describe the transformations on the pink graph and write an equation for it?

I don't like trial and error method, I would prefer if you can explain another method.

Answer 1

Observe what is the same about the two; also observe what is different. Quantify these differences (put numbers to them).
Picture the transformations you could do to that would enact these differences.

`y = f(–1/2(x - 2)) - 3`.

Explanation:

We first observe that the pink graph is wider left-to-right than the orange graph. This means we must have dilated (or stretched) the orange graph horizontally at some point.

We also observe that both the pink and orange graphs have the same height (4 units). This means there was no vertical dilation of the orange graph.

The pink graph is also lower than the orange graph. This means either a vertical translation (aka "shift") or a vertical flip has occurred.

What confused me was how it appeared as though the transformation involved a vertical flip, but I couldn't get that to work, because the line segments in the orange graph have widths of `3:1:2`, while the pink's are `4:2:6`. No horizontal stretch can get `3:1:2` to line up with `4:2:6`. I was stumped.

But then...

I noticed that I could get `3:1:2` to match `6:2:4` (the widths of the pink lines in reverse) by multiplying by 2. This suggested that a horizontal flip and a horizontal dilation (by a factor of 2) had occurred.

I started picturing it. "If we flip `f(x)` horizontally to `f(–x)`, then stretch that left-to-right by a factor of 2 to `f(–x/2)`," I said to myself, "then the orange graph will have the same shape and size as the pink one." The only thing left would be to translate it so that it went where the pink one was.

I remembered that horizontal flips and horizontal dilations do not move any point that is on the `y`-axis. And I noticed that the orange graph has a vertex on that axis! This highest point of the orange graph would need to move 2 units right and 3 units down to coincide with the highest point on the pink graph.

Thus, the final transformation can be written as:

`y = f(color(orange)(–)color(blue)(1/2)(x - color(green)2)) - color(magenta)3`

where:

the `color(orange)(–)` indicates a horizontal flip,
the `color(blue)(1/2)` indicates a left-right stretch by 2,
the `color(green)(-2)` indicates a translation to the right by 2, and
the `color(magenta)(-3)` indicates a translation down by 3.

---

I wish there were a step-by-step method that would always guarantee success, but sometimes "trial and error" is the only way to make progress on these things. In general, though, try to find stretches and flips first, and then find shifts (as needed).

Again, notice what is the same between the two graphs, and notice what is different. Try to find how to quantify these differences, then put them together to create the total transformation.

Most importantly, never be afraid to make mistakes. To paraphrase inventor Thomas Edison, the "error" in trial-and-error isn't failing; it's successfully finding things that don't work! :D