Question

How do I find the tangent line of this function at x=1? y = f(x) = ln(x^2 + 4x + 1) Please show working!! I'm super confused

Answer 1

`y=x+ln6-1`

Explanation:

.

To find the slope of the tangent to the curve at a specific point, we take the derivative of its function and evaluate it at that point:

`y=ln(x^2+4x+1)`

Let `u=x^2+4x+1, :. (du)/dx=2x+4, and y=lnu`

`(dy)/(du)=(d(lnu))/(du)=1/u`

`dy/dx=(dy)/(du)*(du)/(dx)`

`dy/dx=1/u*(2x+4)=(2x+4)/(x^2+4x+1)`

Now, we evaluate this derivative for `x=1`

`Slope=m=(2(1)+4)/((1)^2+4(1)+1)=6/6=1`

Now, we write the equation of the straight line tangent to the curve, which is in the form of :

`y=mx+b`

`y=(1)x+b`

`y=x+b`

`b` is the `y`-intercept of the line and can be found by plugging in the coordinates of the tangency point. But we need to find the `y`-coordinate of the point of tangency first by plugging `x=1` into the function:

`y=ln6`

Therefore, the point of tangency has the coordinates of:

`(1, ln6)`

Now we plug these into the equation of the tangent line:

`ln6=1+b`

`b=ln6-1`

Therefore, the equation of the tangent line is:

`y=x+ln6-1`

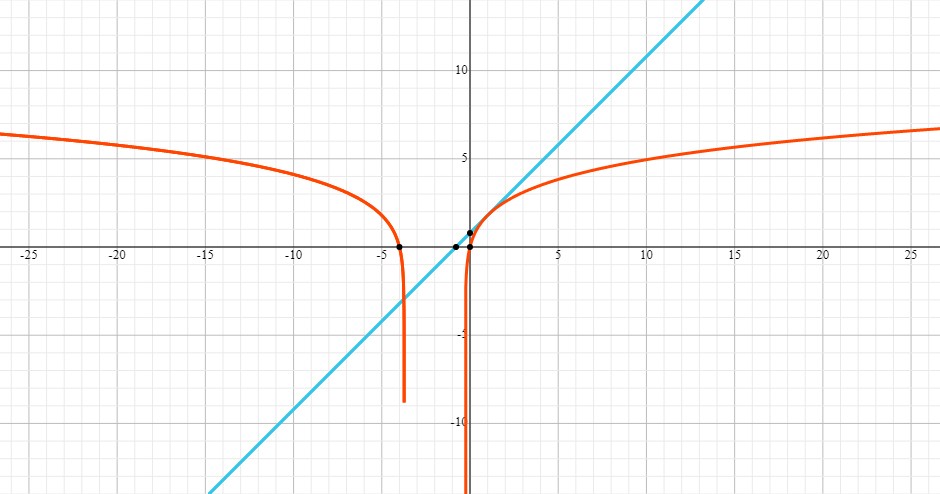
Here are the graphs of the function and the tangent at `x=1`: