Question

`tildenu = c - R_H / n_2^2` (`tildenu = "wavenumber"`) This equation can be written in the form `y = mx + c` What will the intercept of the line on the `y` axis (at `x = 0`) be, in terms of `n_1`?

Answer 1

The y-intercept is:

`c = R_H/n_1^2`

assuming this is for a fixed starting quantum level `n_1`.

For example, if we obtained frequencies from a hydrogen absorption spectrum based on excitations from an unknown `n_1` to a guess of `n_2 = 3,4,5,6,7`, and the peaks are all of VERY low intensity, then we get:

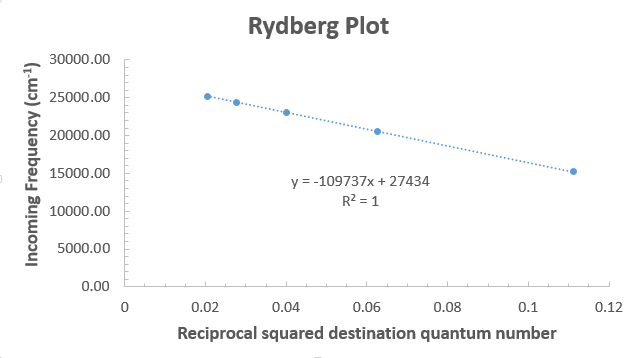
From this, the slope is `E_1 = -R_H` and the y-intercept is `R_H/n_1^2`.

Since `R_H = "109737 cm"^(-1)`,

`n_1 = sqrt(R_H/c) = sqrt("109737 cm"^(-1)/("27434 cm"^(-1))) = 2.000002 ~~ 2`

So, the starting quantum level was `n_1 = 2`.

• Had we guessed `n_2 = 4,5,6,7,8`, we would get `n_1 = 2.721963`, with an `R^2 = 0.9961`.
• Had we guessed `n_2 = 5,6,7,8,9`, we would get `n_1 = 3.465822`, with an `R^2 = 0.9886`.
• Had we guessed `n_2 = 6,7,8,9,10`, we would get `n_1 = 4.229976`, with an `R^2 = 0.9807`.

Lastly, because the peaks were of very low intensity, it couldn't be that `n_1 = 1` because that is the usual occupation of the lowest-energy electron in the hydrogen atom. Low-intensity peaks suggest that the electron started in an excited state.

(You really can tell when you've not correctly guessed the lowest `n_2`.)

---

If you want to plot

`tildenu = c - R_H/(n_2^2)`

you would use `tildenu -= y` and `1/n_2^2 -= x`. I suppose this could be rewritten in the usual Rydberg equation form as:

`overbrace(tildenu)^(y) = -R_H(1/n_2^2 - c/(R_H))`

`= overbrace(-R_H)^"slope" cdot overbrace(1/n_2^2)^(x) + overbrace(c)^("y-intercept")`

where `R_H = "109737 cm"^(-1)` is the Rydberg constant.

We compare with the actual equation:

`tildenu = -R_H(1/n_2^2 - 1/n_1^2)`

From this, we see that

`c/R_H = 1/n_1^2`

Therefore, the y-intercept would be:

`color(blue)(c = R_H/n_1^2)`

and the slope would be the ground state energy of hydrogen atom, `-"109737 cm"^(-1)`.