Please can you help with a question on probability from the Venn diagram given. ?
3 Answers
Choice (4)
Explanation:
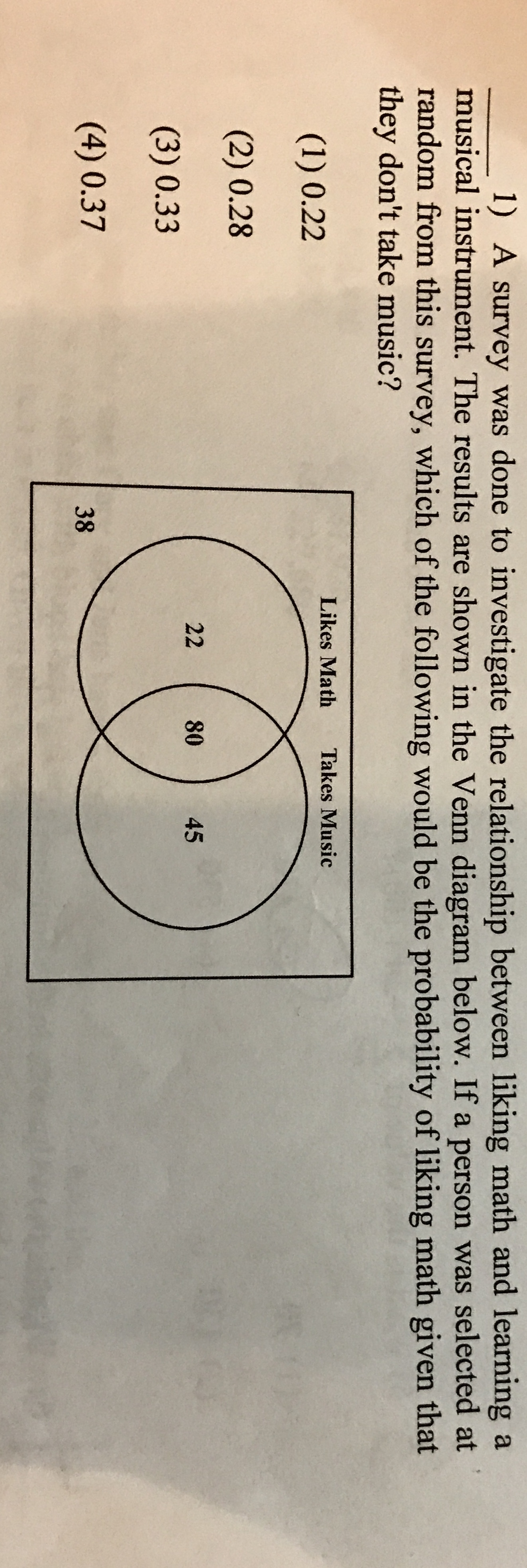
It is given that the random person chosen for this survey does not take music. So the middle value (80, where the person likes both math and takes music) is out. Obviously, the 45 is also out because that is the part of the circle where the person only takes music.
What is left is the 22 (where the person only likes math), and the 38 which is in neither circle (meaning they neither like math nor takes music).
So, to find the probability, we are going to divide the number of people who like math (22), by the total people excluding those who play an instrument (22 + 38).
Now for some arithmetic:
And for the sake of not having a repeating decimal for your answer, we will round it to hundredths:
Explanation:
This question involves conditional probability—the chance of an event
Normally, when we consider just the probability of
#"P"(A) = ("size of "A)/("size of "S)#
and thought of as the fraction of
When we have a conditional probability, such as the probability of
So, when we take the probability
#"P"(A|B) = ("size of "(AnnB))/("size of "B)#
and thought of as the fraction of
Solution:
In the given question, our sample space has a size of
#|S|=38+22+80+45#
#color(white)(|S|)=185#
Of these 185 students, 125 take music (80 + 45), while the other 60 do not (38 + 22).
Since we are interested in
Now, of these 60 students that don't take music, how many also like math? From the Venn diagram, that's easy to see; it's 22. So, our conditional probability is:
#"P"("Math" | "NOT Music")#
# = ("size of "("Math" nn "NOT Music"))/("size of (NOT Music)")#
# = 22/60# ,
which reduces to
answer 4
Explanation:
there are 38 who do not take music and do not like maths.
there are 22 who like maths but do not take music
so you have 38+22=60 people who do not take music
the probability of the chosen person liking maths is
this rounds to 0.37