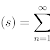If #lim_(x rarr oo)((ax^2+bx+3)^(1/2) -2x)=7#, then find #a# and #b#?
1 Answer
May 17, 2018
Explanation:
Complete the square underneath the radical to get:
Okay, so we have this equivalent form, and note that this is the equation of the line, and so for it to have a finite limit of seven, the
Thus
In this case our limit becomes
So in fact this is satisfied only by