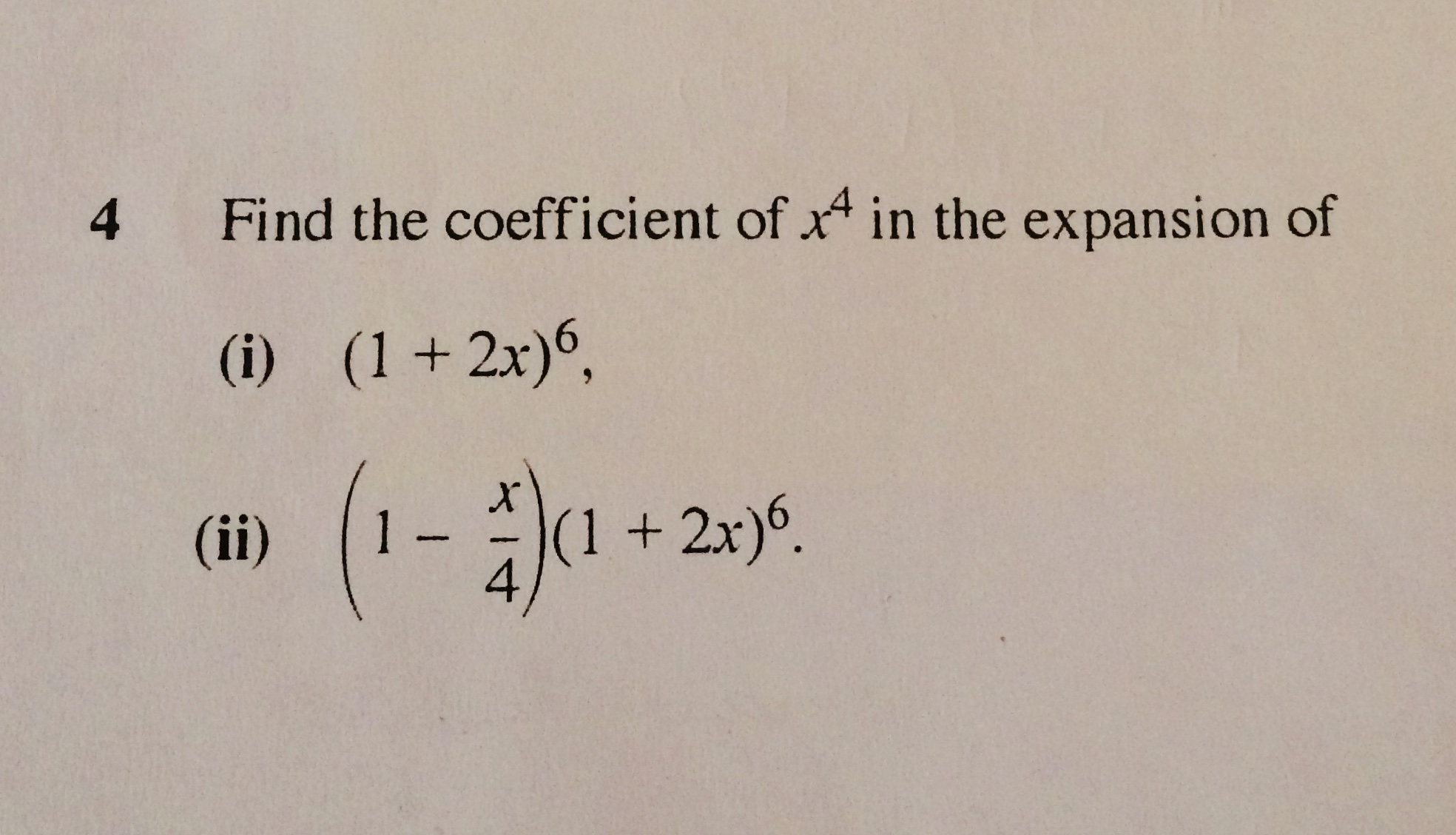We can do this by using Pascal's Triangle, shown below.

(i)
Since the exponent is #6#, we need to use the sixth row in the triangle, which includes #color(purple)(1, 6, 15, 20, 15, 6)# and #color(purple)1#. Basically, we will use #color(blue)1# as the first term and #color(red)(2x)# as the second. Then, we can create the following equation. The exponent of the first term increases by #1# each time and the exponent of the second term decreases by #1# with each term from the triangle.
#(color(purple)1*color(blue)(1^0)*color(red)((2x)^6))+(color(purple)6*color(blue)(1^1)*color(red)((2x)^5))+(color(purple)15*color(blue)(1^2)*color(red)((2x)^4))+(color(purple)20*color(blue)(1^3)*color(red)((2x)^3))+(color(purple)15*color(blue)(1^4)*color(red)((2x)^2))+(color(purple)6*color(blue)(1^5)*color(red)((2x)^1))+(color(purple)1*color(blue)(1^6)*color(red)((2x)^0))#
Then, we can simplify it.
#64x^6+192x^5+240x^4+160x^3+60x^2+12x+1#
Therefore, the coefficient of #x^4# is #240#.
(ii)
We already know the expansion of #(1+2x)^6#. Now, we can multiply the two expressions together.
#color(brown)(1-x(1/4))*color(orange)(64x^6+192x^5+240x^4+160x^3+60x^2+12x+1)#
The coefficient of the #x# in #1-x(1/4)# is #1#. So, we know that it will raise the values of the exponents in the other expression by #1#. Because we need the coefficient of #x^4#, we just need to multiply #160x^3# by #1-x(1/4)#.
#160x^3-40x^4#
Now, we need to add it #240x^4#. This is one part of the solution of #240x^4*(1-x(1/4))#, due to the multiplication by #1#. It is significant because it also has an exponent of #4#.
#-40x^4+240x^4=200x^4#
Therefore, the coefficient is #200#.