My question is: "find the particular solution y(x) of the given differential equation which complies with the initial condition" # xy'+x^2=2y# with #y(1)=0# How to solve it? Thank you!
here:
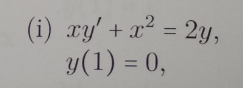
this should be solution:
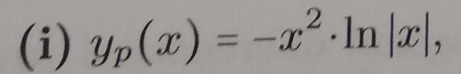
here:
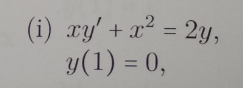
this should be solution:
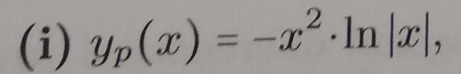
1 Answer
# y = -x^2 \ ln |x| #
Explanation:
We have:
# xy'+x^2=2y# with#y(1)=0#
We can use an integrating factor when we have a First Order Linear non-homogeneous Ordinary Differential Equation of the form;
# dy/dx + P(x)y=Q(x) #
So, we can put the equation in standard form:
# xy'-2y = -x^2#
# :. y'- (2y)/x = -x# ..... [A]
Then the integrating factor is given by;
# I = e^(int P(x) dx) #
# \ \ = exp(int \ -2/x \ dx) #
# \ \ = exp(-2ln|x| ) #
# \ \ = e^(ln|x|^(-2)) #
# \ \ = 1/x^2 #
And if we multiply the DE [A] by this Integrating Factor,
# :. 1/x^2 \ y' - 1/x^2 \ (2y)/x = 1/x^2 \ (-x) #
# :. 1/x^2 \ y' - 2/x^3 \ y = -1/x #
# :. d/dx (y/x^2) = -1/x #
This is now separable, so by "separating the variables" we get:
# y/x^2 = int -1/x \ dx + C #
Which is trivial to integrate to get the General Solution:
# y/x^2 = -ln | x| + C #
Applying the initial condition
# 0/1 = -ln | 1| + C => C = 0#
Leading to the Particular Solution:
# y = x^2(-ln | x| + 0) #
# :. y = -x^2 \ ln |x| \ \ \ # QED

