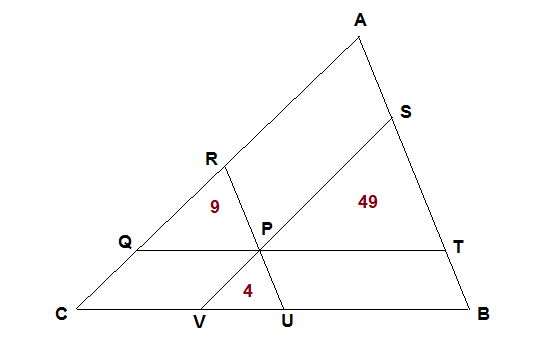
We know that the ratio of areas of two similar triangle is equal to the squares of the ratio of lengths of their corresponding sides.
Here #Delta ABC# is similar to #DeltaPQR,DeltaPST and DeltaPUV#
So #(DeltaPQR)/(Delta ABC)=(PR)^2/(AB)^2#
#=>9/(Delta ABC)=(AS)^2/(AB)^2#
#=>sqrt(9/(Delta ABC))=(AS)/(AB)#
#=>3/sqrt(Delta ABC)=(AS)/(AB).......[1]#
Similarly
#(DeltaPST)/(Delta ABC)=(ST)^2/(AB)^2#
#=>49/(Delta ABC)=(ST)^2/(AB)^2#
#=>sqrt(49/(Delta ABC))=(ST)/(AB)#
#=>7/sqrt(Delta ABC)=(ST)/(AB).......[2]#
And also
#(DeltaPUV)/(Delta ABC)=(PU)^2/(AB)^2#
#=>4/(Delta ABC)=(BT)^2/(AB)^2#
#=>sqrt(4/(Delta ABC))=(BT)/(AB)#
#=>2/sqrt(Delta ABC)=(BT)/(AB).......[3]#
Adding {1] ,[2] and [3] we get
#3/sqrt(Delta ABC)+7/sqrt(Delta ABC)+2/sqrt(Delta ABC)=(AS)/(AB)+(ST)/(AB)+(BT)/(AB)#
#=>12/sqrt(Delta ABC)=(AS+ST+BT)/(AB)=(AB)/(AB)=1#
#=>DeltaABC=12^2=144#



