Question

Prove that given a line and point not on that line, there exactly one line that passes through that point perpendicular through that line? You can do this mathematically or through construction (the ancient Greeks did)?

Answer 1

See Below.

Explanation:

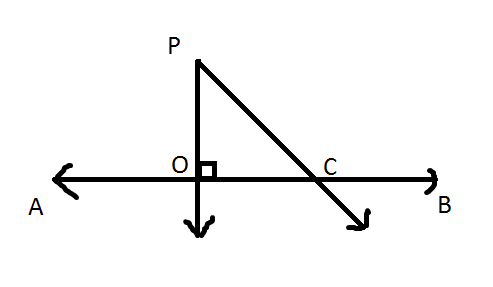
Let's Assume That The Given Line is `AB`, and the point is `P`, which is not on `AB`.

Now, Let's assume, We have drawn a perpendicular `PO` on `AB`.

We have to prove that, This `PO` is the only line passing through `P` that is perpendicular to `AB.`

Now, we will use a construction.

Let's construct another perpendicular `PC` on `AB` from point `P`.

Now The Proof.

We have,

`OP` perpendicular `AB` [I can't use the perpendicular sign, how annyoing]

And, Also, `PC` perpendicular `AB`.

So, `OP` || `PC`. [Both are perpendiculars on the same line.]

Now Both `OP` and `PC` have point `P` in common and they are parallel.

That means, they should coincide.

So, `OP` and `PC` are the same line.

Thus, There is only one line passing through point `P` that is perpendicular to `AB`.

Hope this helps.