Question

How do you use synthetic division to find all roots of `x^3 + 5x^2 + 3x -9 = 0`?

Answer 1

`(x-1)(x+3)^2`

`x=1,color(white)("dd") ubrace(x=-3 and x=-3)`
`color(white)("dddddddddddddd.d")uarr`
`color(white)("dddddddddddd")" duplicity"`

Explanation:

Whole number factors of 9 are `3^2 and 1xx9`

Lets test for `x=+1`

`(+1)^3+5(+1)^2+3(+1)-9`
`color(white)("dd")1color(white)("dd.")+color(white)("dd")5color(white)("dd.d")+color(white)("dd")3color(white)("dd.")-9=0` as required

So we have `(x-1)` as a factor.

To determine the related quadratic divide by `(x-1)`

`(x^3+5x^2+3x-9)/(x-1)=0=" some quadratic"`

The coefficients for `x^3+5x^2+3x-9color(white)("dd")->color(white)("dd")1,5,3,-9`

`color(white)("d")1|1color(white)("d")5color(white)("d")3color(white)("d")-9 color(white)("d")larr" The coefficients"`
`color(white)("dd.")ul(|darr1color(white)("d")6color(white)("ddd.")9)`
`color(white)("dddd")1 color(white)("d") 6color(white)("d")9color(white)("ddd")0color(white)("d")->color(white)("d")1x^2+6x+9`

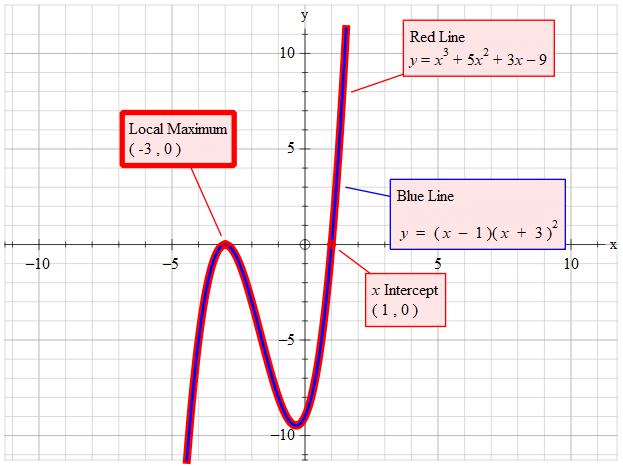
So we have:

`(x-1)(x^2+6x+9)=0`

Note that `3xx3=9 and 3+3=6`

`(x-1)(x+3)^2=0`