Check below? (geometry involved)
Given isosceles triangle #AhatBC# #(AB=AC)# circumscribed in a circle with radius #r=1# .
Consider #x# the height of the triangle #AhatBC# from the vertex #A# .
-
#a)# Prove that #BC=2sqrt(x/(x-2))# #color(white)(aa)# , #x>2#
-
#b)# Find the value of #x# for which the area of the triangle #AhatBC# is minimum
-
#c)# The side #BC# of the triangle is changing with a rate of #sqrt3# #(cm)/sec# . Find the rate of change for the angle #hatA# when the triangle becomes equilateral
(Area is given as a function of #x# )
Given isosceles triangle
Consider
-
#a)# Prove that#BC=2sqrt(x/(x-2))# #color(white)(aa)# ,#x>2# -
#b)# Find the value of#x# for which the area of the triangle#AhatBC# is minimum -
#c)# The side#BC# of the triangle is changing with a rate of#sqrt3# #(cm)/sec# . Find the rate of change for the angle#hatA# when the triangle becomes equilateral
(Area is given as a function of
4 Answers
PART a):
Explanation:
Have a look:
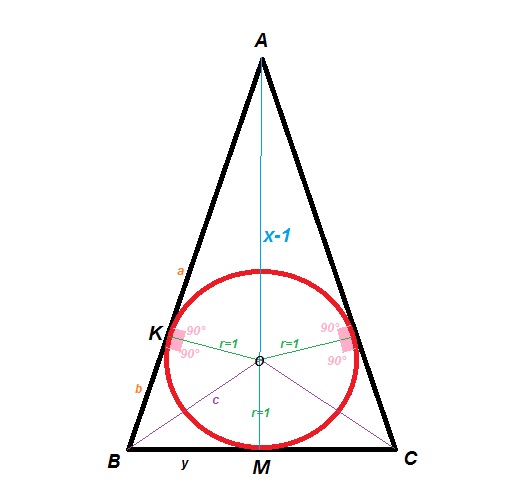
I tried this:

PART b): (but check my maths anyway)
Explanation:
Have a look:
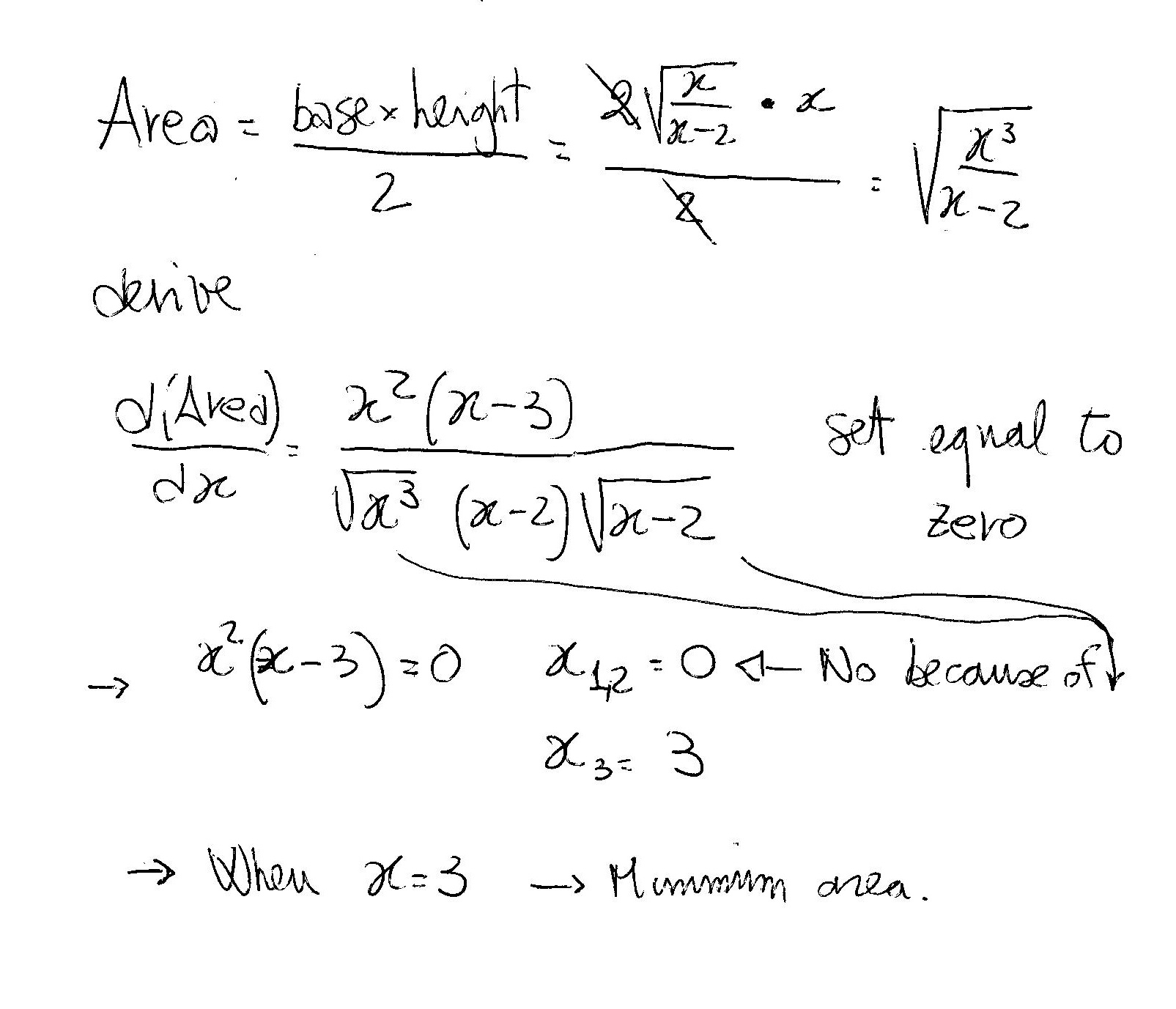
PART c) BUT I am not sure about it...I think it is wrong...
Explanation:
Have a look:

Part c
Explanation:
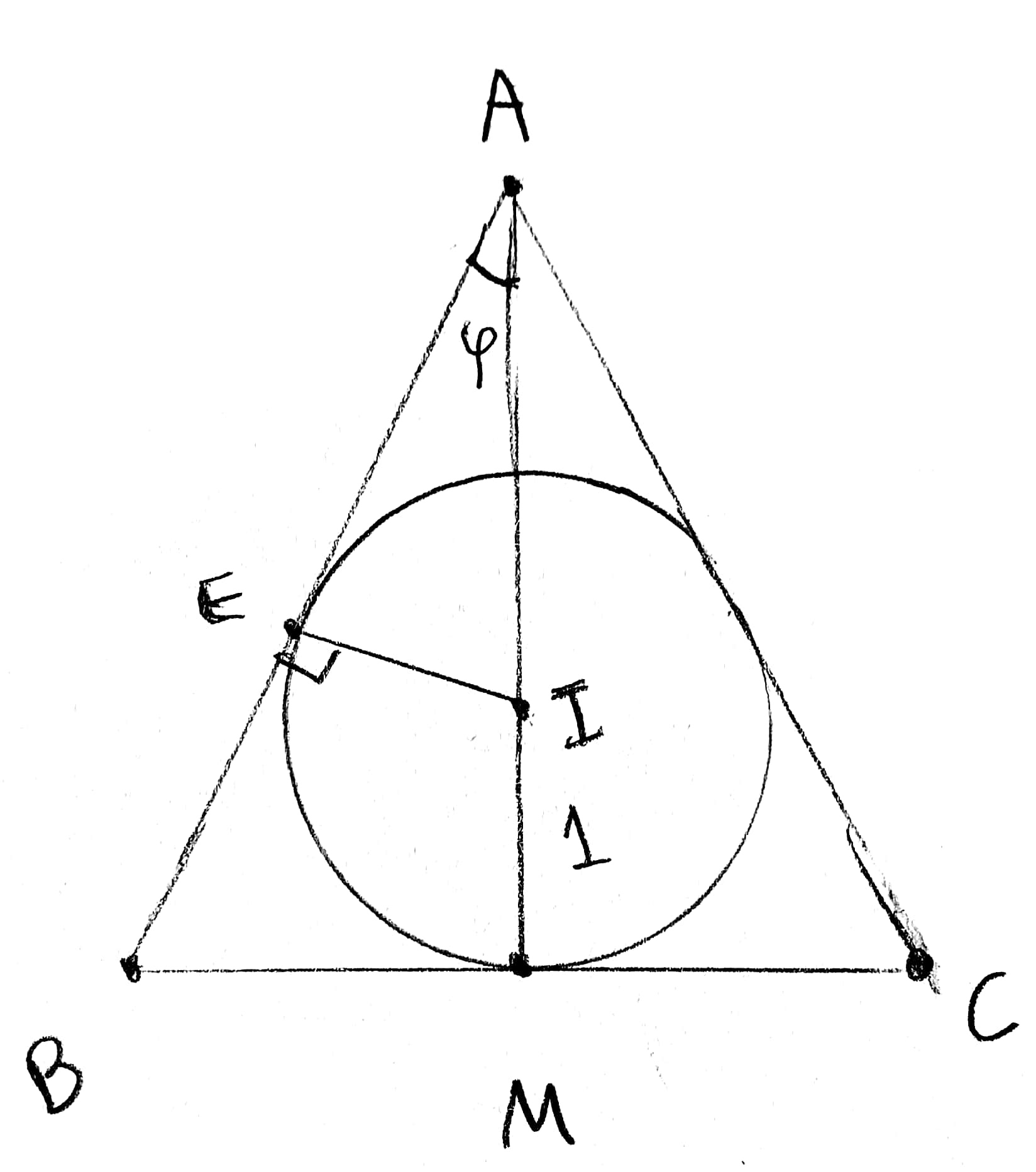
Take into account that while the base
Based on the above,
Consider
We have
-
#ΔAEI# :#sinφ=1/(AI)# #<=># #AI=1/sinφ# -
#AM=AI+IM=1/sinφ+1=(1+sinφ)/sinφ#
In
Differentiating in respect to
For
and
Thus, since
we have
But
therefore,
(Note: The moment when the triangle becomes equilateral


