Question

How do you solve `abs(20+1/2x)>6`?

Answer 1

See a solution process below:

Explanation:

The absolute value function takes any term and transforms it to its non-negative form. Therefore, we must solve the term within the absolute value function for both its negative and positive equivalent.

`-6 > 20 + 1/2x > 6`

`-6 - color(red)(20) > 20 - color(red)(20) + 1/2x > 6 - color(red)(20)`

`-26 > 0 + 1/2x > -14`

`color(red)(2) xx -26 > color(red)(2) xx 1/2x > color(red)(2) xx -14`

`-52 > color(red)(2)/2x > -28`

`-52 > 1x > -28`

`-52 > x > -28`

Or

`x < -52`; `x > -28`

Or, in interval notation:

`(-oo, -52)`; `(-28, +oo)`

Answer 2

`x <-52` or `x > -28`

Explanation:

One way to approach the evaluation of an absolute value inequality like `abs(20+1/2x) > 6` is to first temporarilly replace `(20+1/2x)` with some other variable.
For example if we let `z=(20+1/2x)` then we have the simpler inequality:
`color(white)("XXX")abs(z) > 6`
Presented on the number line this would look like:

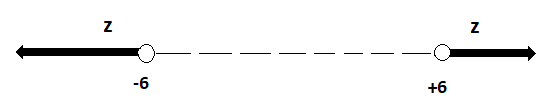
That is
`color(white)("XXXxxxxxx")z < -6color(white)("xxxx")"or"color(white)("xxxxxxxxx") z > +6`
then since we know `z=20+1/2x`
these become
`color(white)("XXX")20+1/2x < -6color(white)("xxxx")"or"color(white)("xxxx") 20+1/2x > +6`

`color(white)("XXX20+")1/2x < -26color(white)("xxxx")"or"color(white)("xxxx20+") 1/2x > -14`

`color(white)("XXX"20+2)x < -52color(white)("xxxx"20+2)"or"color(white)("xxxx") x > -28`