.
#color(red)(a))#
#y=2/(2-x)#
#P(3,-2)#, #Q(x, 2/(2-x))#
The slope of line PQ can be calculated for each #x#-value using:
#m_(PQ)=(y_Q-y_P)/(x_Q-x_P)#
#x=2.9, :. y=2/(2-2.9)=2/(-0.9)=-2.222222, :. m_(PQ)=(-2.222222-(-2))/(2.9-3)=(-0.222222)/(-(0.1))=color(red)(2.222222)#
#x=2.99, :. y=2/(2-2.99)=2/(-0.99)=-2.020202, m_(PQ)=(-2.020202-(-2))/(2.99-3)=(-0.020202)/(-0.01)=color(red)(2.020202)#
Much the same way:
#x=2.999, :. y=-2.002002, m_(PO)=color(red)(2.002002)#
#x=2.9999, :. y=-2.00020002, m_(PO)=color(red)(2.000200)#
#x=3.1, :. y=-1.818181, m_(PQ)=color(red)(1.818181)#
#x=3.01, :. y=-1.980198, m_(PQ)=color(red)(1.980198)#
#x=3.001, :. y=-1.998001, m_(PQ)=color(red)(1.998001)#
#x=3.0001, :. y=-1.999800, m_(PQ)=color(red)(1.999800)#
#color(red)(b))#
As we can see from part #a)#, the values of the slope #m# converge from both directions to #2#. Therefore,
#color(red)(m_(PQ)=2)#
#color(red)(c))#
The equation of the tangent line to the curve is:
#y=mx+b# where #m# is the slope and #b# is the #y#-intercept:
#y=2x+b#
We can use the coordinates of point #P# to solve for #b#:
#-2=2(3)+b#
#-2=6+b#
#b=-8#
Therefore, the equation of the tangent line is:
#color(red)(y=2x-8)#
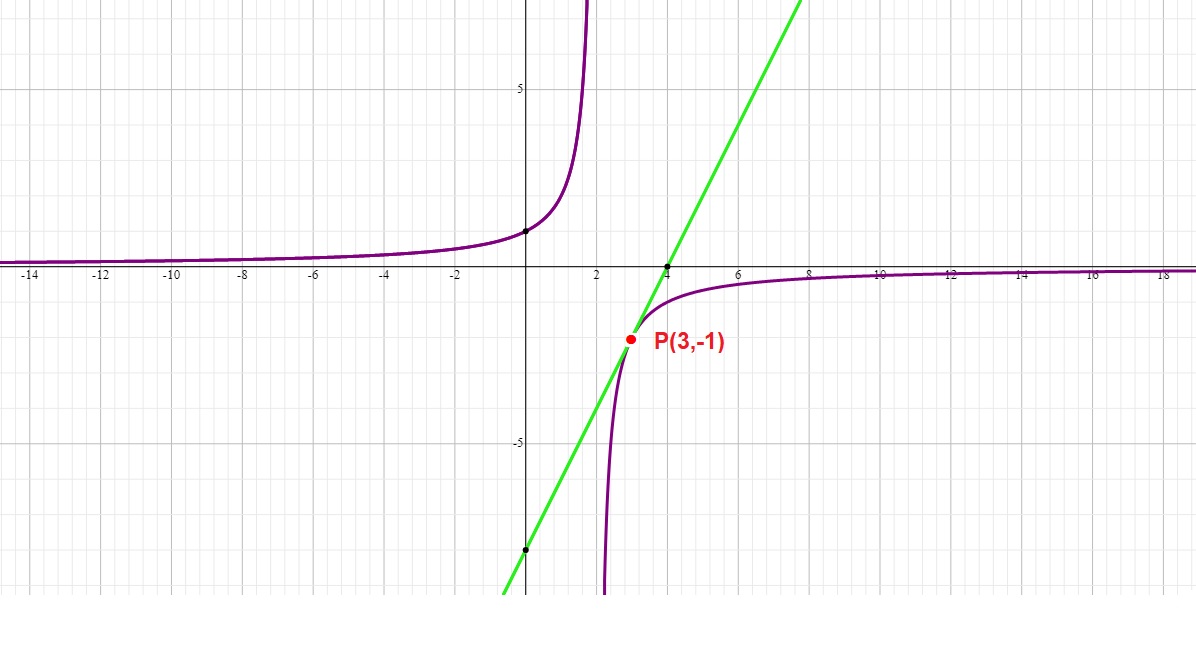
The graph below shows the function and the tangent to it at point #P#: