Given the functions #a(x) = 4x2 + 2x − 3# and #b(x) = x − 1#, identify the oblique asymptote of #a(x)/b(x)#?

1 Answer
Sean
May 31, 2018

Please see below.

Explanation:

.

I think you meant to input:

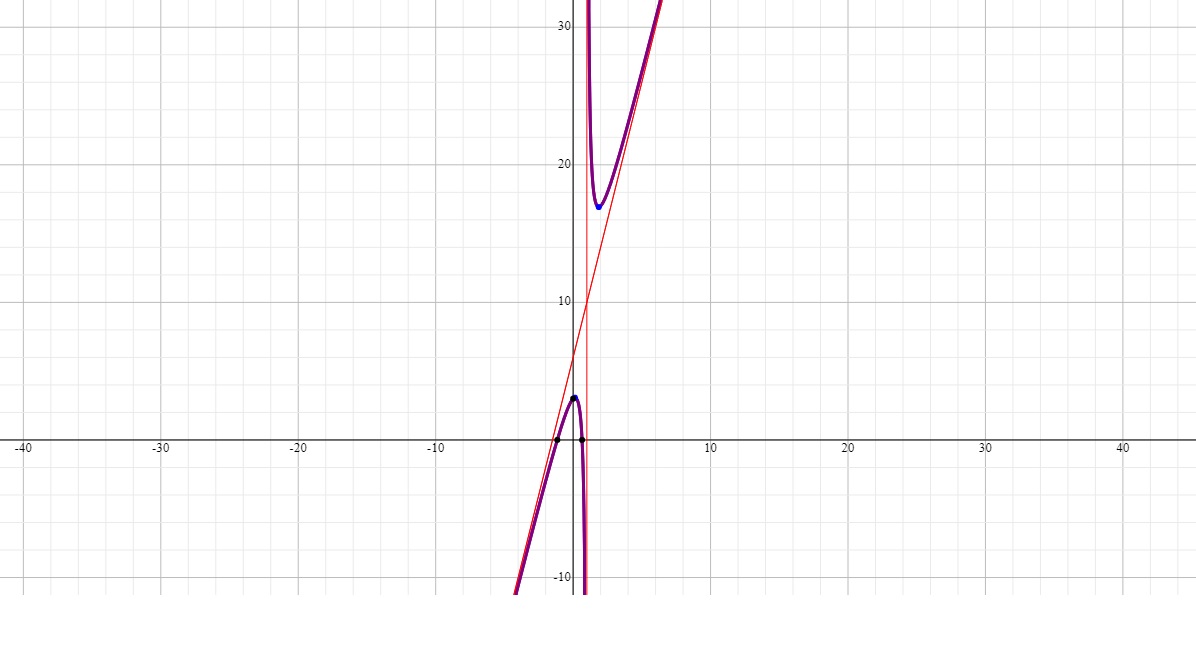
Identify the oblique asymptote of #(a(x))/(b(x))#.

The oblique (slant) asynptote exists when the degree of the numerator is one more than the degree of the denominator. You need to perform long division to find it:

#(a(x))/(b(x))=(4x^2+2x-3)/(x-1)=4x+6+3/(x-1)#

The equation of the oblique asymptote is:

#y=4x+6#

The graph below depicts the above solution:

enter image source here

Related questions
Impact of this question
4449 views around the world
You can reuse this answer
Creative Commons License