Question

Which definite integral would you use to compute the area enclosed by the parabola y=-x^2+4 and the line y=2x-3?

Answer 1

`color(blue)[A=int_(-3.828)^(1.828)(-x^2-2x+7)*dx`

Explanation:

the area Between two curves due to `"x-axis"` given by:

`color(red)[A=int_a^by_2-y_1*dx`

where `y_2` is the curve in the top and `y_1` is the curve bottom.

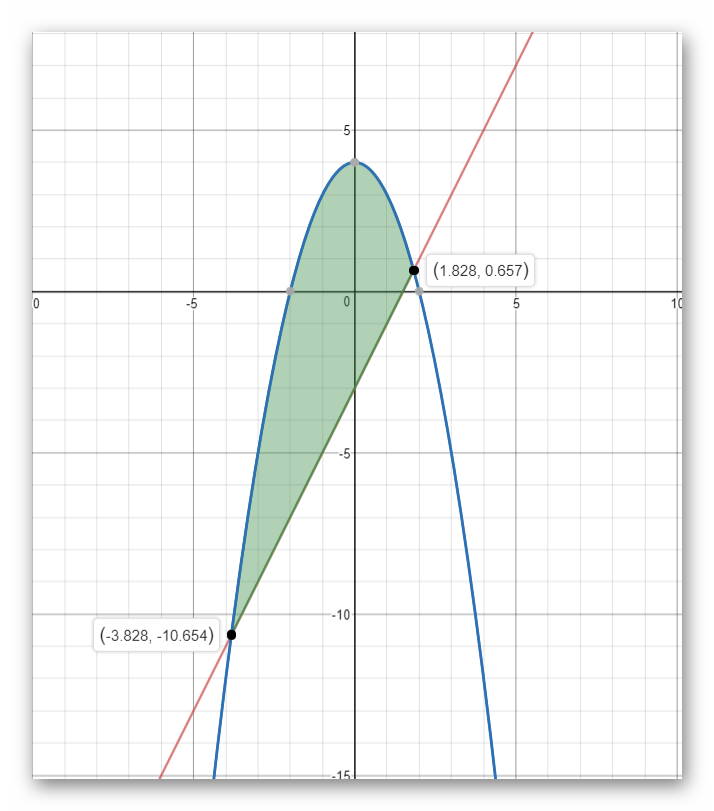
in your question the area between the curves is given by:

`color(blue)[A=int_(-3.828)^(1.828)(-x^2+4)-(2x-3)*dx`

`color(blue)[A=int_(-3.828)^(1.828)(-x^2-2x+7)*dx`

show the figure below the area between the two curves:

to find the cross between the curve :

`y_2=y_1`

`-x^2+4=2x-3`

`x^2+2x-7=0`

After solving it you will get:

`x=-3.828 or x=1.828`