Two people meet in the purple room on the fourth floor of a building. On departure, one person travels West 16 feet, South 9 feet, and Down 9 feet. The other person travels North 16 feet, East 8 feet, and Up 9 feet. How far apart are the two people? Round
1 Answer
I get
If you want me to round to the nearest integer, it would actually be about
Interestingly enough, the distances each person walked were
(In fact, it is
Well, let's draw this out in 3D space to see what is asked for. I assume up/down refers to altitude (
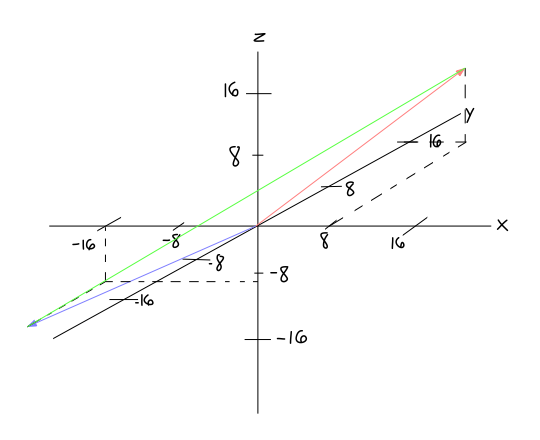
Suppose person
The point that they land upon is a vector.
#color(blue)(vecv_1) = << -16, -9, -9 >>#
#color(red)(vecv_2) = << +16, +8, +9 >>#
Do not simply add the vectors together as they are:
#color(blue)(vecv_1) + color(red)(vecv_2) = << 0, -1, 0 >>#
What we actually need to do is reverse the vector
Thus, what we should do is add
#color(green)(vecv_3) = -color(blue)(vecv_1) + color(red)(vecv_2)#
#= - << -16, -9, -9 >> + << +16, +8, +9 >>#
#= << +16, +9, +9 >> + << +16, +8, +9 >>#
#= << +32, +17, +18 >>#
Lastly, we need to find the length of this vector to determine the distance:
#color(green)(|vecv_3|) = sqrt(x^2 + y^2 + z^2)#
#= sqrt(("32 ft")^2 + ("17 ft")^2 + ("18 ft")^2)#
#=# #color(green)("40.5 ft")#

