Question

A triangle has corners at `(5 ,6 )`, `(4 ,3 )`, and `(2 ,5 )`. What is the area of the triangle's circumscribed circle?

Answer 1

`color(blue)((25pi)/8" units squared")`

Explanation:

The vertices of the triangle all lie on the circumference of the circumscribed circle. In order to find the area of the circle we need to find its radius.

The general equation of a circle is given as:

`(x-h)^2+(y-k)^2=r^2`

Where `bbh` and `bbk` are the x and y coordinates of the centre respectively.

We have three point so we can construct three different equations:

`(5-h)^2+(6-k)^2=r^2 \ \ \ \[1]`

`(4-h)^2+(3-k)^2=r^2 \ \ \ \[2]`

`(2-h)^2+(5-k)^2=r^2 \ \ \ \[3]`

Solving simultaneously:

Subtract `[2]` form `[1]`

`9-2h+27-6k=0`

`36-2h-6k=0 \ \ \ \[4]`

Subtract `[3]` from `[2]`

`12-4h-16+4k=0`

`-4-4h+4k=0 \ \ \ \[5]`

Using `[5]`

`h=k-1`

Substituting in `[4]`

`36-2(k-1)-6k=0=>k=19/4`

Substituting in `h=k-1`

`h=19/4-1=>h=15/4`

We now have the coordinates of the centre of the circle.

`(15/4,19/4)`

The distance from the centre to any point on the circumference is the radius. Using the distance formula and point `(4,3)`

`|r|=sqrt((15/4-4)^2+(19/4-3)^2)=(5sqrt(2))/4`

Area of circumscribed circle is:

`pi((5sqrt(2))/4)^2=(25pi)/8` units squared

PLOT:

Answer 2

`(25pi)/8`

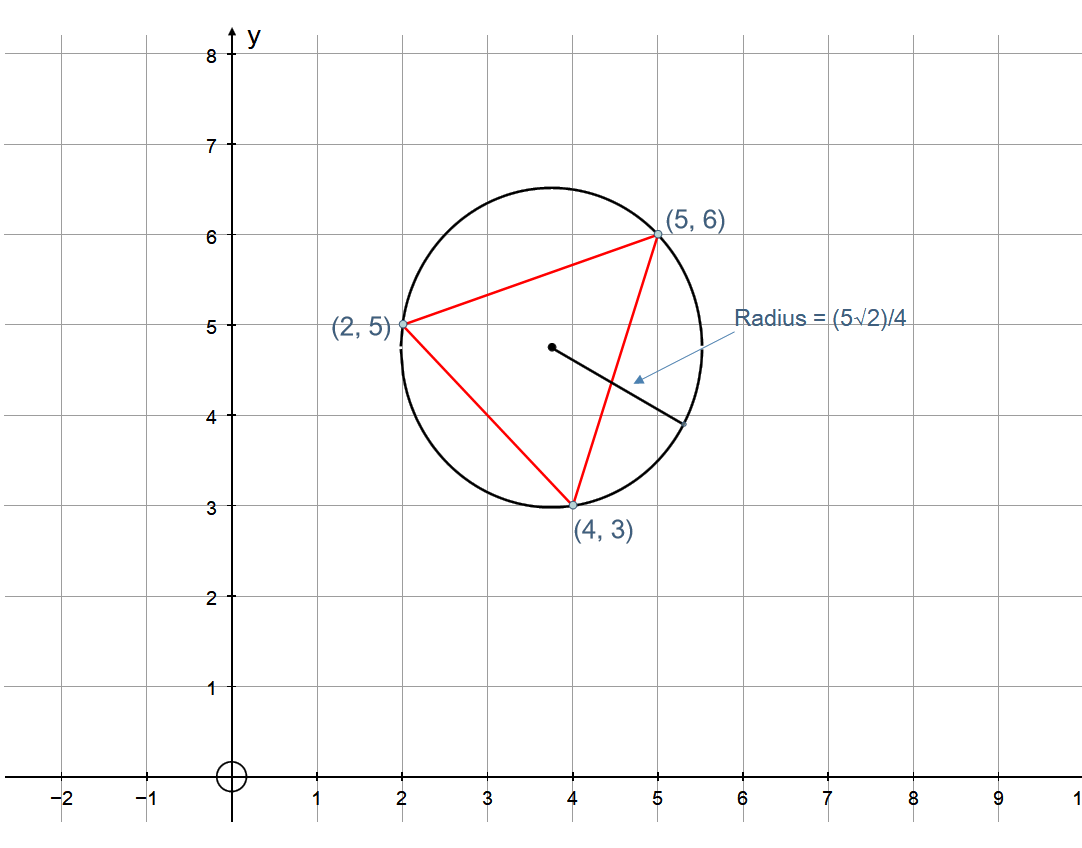
Explanation:

There are no square roots needed.

Archimedes' Theorem says for a triangle with sides `a,b,c:`

`16 \ text{area}^2 = 4a^2b^2-(c^2-a^2-b^2)^2`

The radius of the circumcircle equals the product of the sides of the triangle divided by four times the area of the triangle. This is more useful squared:

`r^2 = {a^2 b^2 c^2}/{16 \ text{area}^2} = {a^2 b^2 c^2}/{ 4a^2b^2-(c^2-a^2-b^2)^2}`

We get `a^2,b^2 and c^2` from `(5,6),(4,3),(2,5)`

`a^2 = (5-4)^2+(6-3)^2=10`

`b^2 = (4-2)^2+(3-5)^2=8`

`c^2=(5-2)^2+(6-5)^2=10`

Isosceles triangle, not that it matters.

`text{circumcircle area} = pi r^2 = pi {10(8)(10) }/{ 4(10)(8) - (10-8-10)^2 } =(25pi)/8`

The other answer is correct, after much more work.