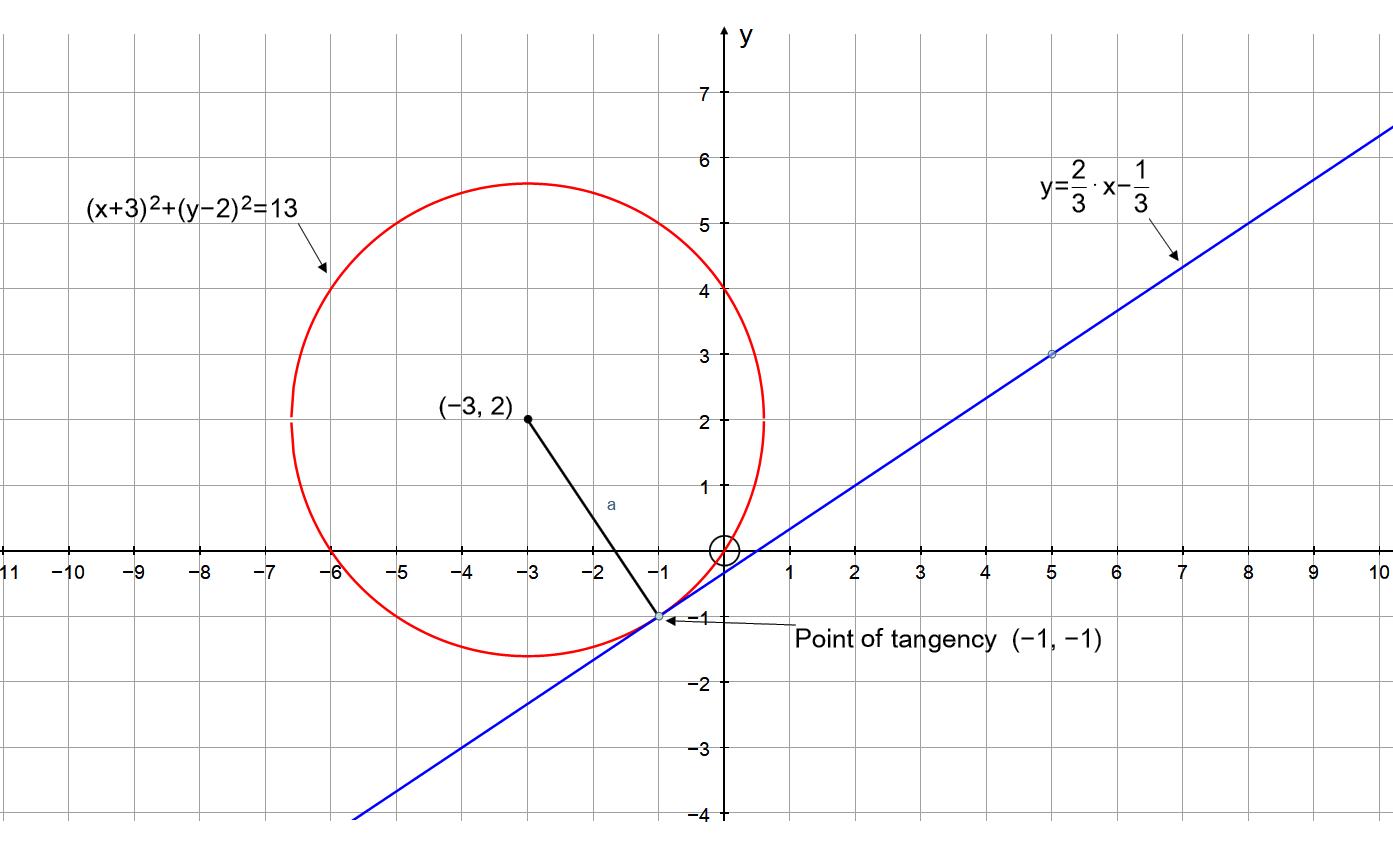
The question is a bit ambiguous. I am assuming you are looking for the equation of the circle with centre at #(-3,2)#.
The standard equation of a circle is given as:
#(x-h)^2+(y-k)^2=r^2#
Where #bbh# and #bbk# are the #bbx# and #bby# coordinates of the centre respectively, and #bbr# is the radius. In order to find this equation we need to find the radius, we already have the coordinates of the centre.
We are told #2x-3y=1# is tangent to the circle. We know the the radius of a circle is perpendicular to the tangent line at the point of tangency. We can therefore exploit this fact to help us find the radius.
If we find the equation of a line that passes through the centre of the circle and is perpendicular to the tangent line, then the point of intersection of these to lines will give us the coordinates of a point on the circumference of the circle and allow us to find the radius.
Rearranging the given equation:
#2x-3y=1=>y=2/3x-1/3#
The gradient is #2/3#. A line that is perpendicular to this, will have a gradient that is the negative reciprocal of this: i.e.
#-3/2#
This line passes through #(-3,2)#.
Using the point slope form of a line:
#(y_2-y_1)=m(x_2-x_1)#
Where #bbm# is the gradient:
#y-2=-3/2(x+3)#
#y=-3/2x-5/2 \ \ \ \[1]#
#y=2/3x-1/3 \ \ \ \ \ \ \ \ [2]#
Solving #[1]# and #[2]# simultaneously:
#2/3x-1/3+3/2x+5/2=0=>x=-1#
Substituting in #[2]#
#y=2/3(-1)-1/3=-1#
So #(-1,-1)# is a point on the circumference. To find the radius, we find the distance between the centre and this point. Using the distance formula:
#|d|=sqrt((x_2-x_1)^2+(y_2-y_1)^2)#
#|d|=sqrt((-3-(-1))^2+(2-(-1))^2)=sqrt(13)#
#"Radius"=sqrt(13)#
Equation of circle is therefore:
#(x+3)^2+(y-2)=(sqrt(13))^2#
#=>(x+3)^2+(y-2)^2=13#
This is the plot of the circle and tangent line: