ABCD is a parallelogram.its vertices B,C and D have the coordinates (-1,-3),(-2,1)and(1,1) respectively.E and F are the middle points of DC and AB respectively.find the equations of the lines AE and CF. IF the Diagonals are AC and BD.?

2 Answers
Soumalya Pramanik
May 28, 2018

The Equation of #AE#:- #144y= -47x + 191#
The Equation of #DF#:- #58y = -63x + 121#

Explanation:

WARNING!! LONG ANSWER!!!!

Made In Paint

First of All,

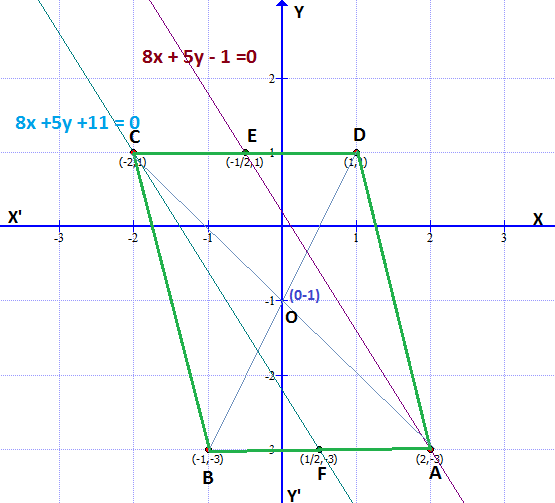
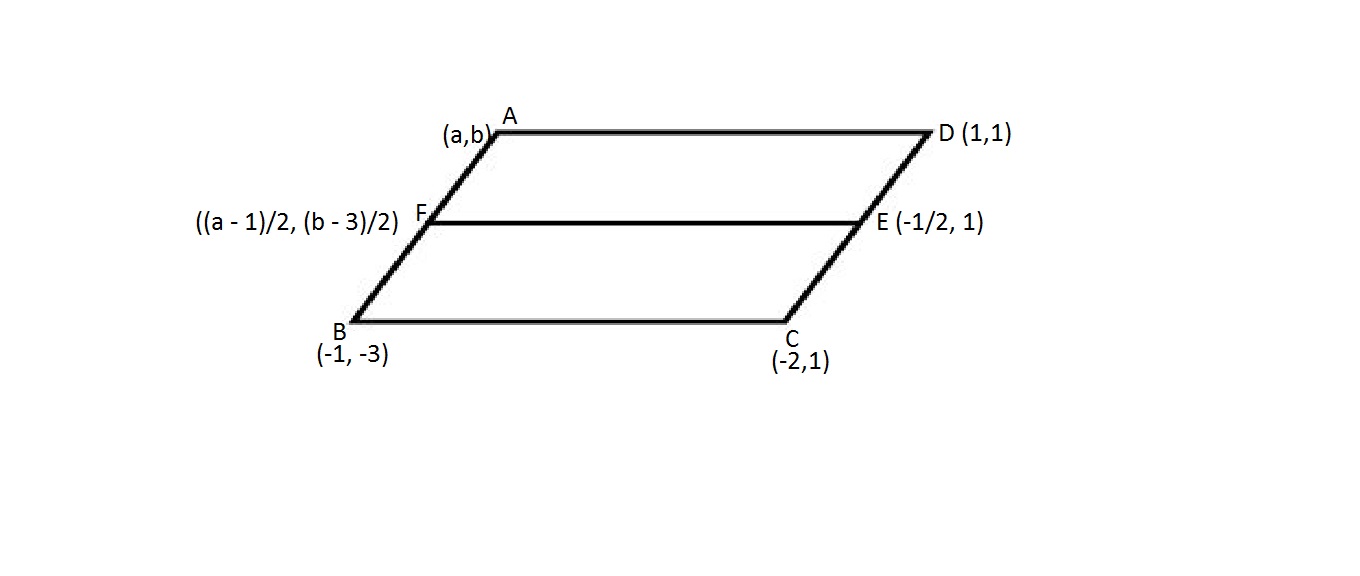
#ABCD# is a parallelogram.

That means the opposite sides of #ABCD# will be parallel and equal.

So, #AB = CD# and #AD = BC#.

Let's assume that The Co-ordinates of Point #A# is #(a, b)#.

Now,

#color(white)(xxx) AB = CD#

#rArr sqrt((a + 1)^2 + (b + 3)^2) = sqrt((-2 -1)^2 + (1 - 1)^2)# [Using the Distance Formula]

#rArr (a + 1)^2 + (b + 3)^2 = (-3)^2 + 0^2#

#rArr a^2 + 2a + 1 + b^2 + 6b + 9 = 9#

#rArr a^2 + 2a + b^2 + 6b = -1# [Transposing the constants to the R.H.S]..........................................................................(i)

Similarly,

#color(white)(xxx) AD = BC#

#rArr sqrt((a - 1)^2 + (b - 1)^2) = sqrt((-1 + 2)^2 + (-3 -1)^2)#

#rArr (a - 1)^2 + (b -1)^2 = 1^2 + (-4)^2#

#rArr a^2 - 2a + 1 + b^2 - 2b +1 = 1 + 16#

#rArr a^2 -2a + b^2 - 2b = 15#.......................................................(ii)

Now, Subtracting (ii) from (i),

#color(white)(xxx)cancel(a^2) + 2a + cancel(b^2) + 6y cancel(-a^2) + 2a cancel(- b^2) + 2b = -1 -15#

#rArr 4a + 8b = -16#

#rArr a + 2b = -4#...................................(iii)

Now, Join #EF#.

As, #E# and #F# are the mid-points of #DC# and #AB# respectively, #BF = FA# and #CE = ED#.

Now, In Quadrilateral #EFCB#,

#BF " | | "CE# and #BF = CE# [As #AB = CD#].

So, #EFCB# is a parallelogram.

Thus, #EF = BC#.

Co-ordinates of #F# = #((a -1)/2, (b -3)/2)# and #E = ((1-2)/2, (1 +1)/2) = (-1/2, 1)#

We will form another equation.

So,

#color(white)(xxx)EF = BC#

#rArr1/2sqrt((a -1)^2 + (b - 3)^2) = sqrt((-1 + 2)^2 + (-3 -1)^2)#

#rArr 1/4((a - 1)^2 + (b - 3)^2) = 1 + 16#

#rArr (a -1)^2 + (b - 3)^2 = 17 xx 4#

#rArr a^2 - 2a +1 + b^2 - 6b + 9 = 68#

#rArr a^2 - 2a + b^2 - 6b = 58#......................................(iv)

Now Subtract (iv) from (i)..

#color(white)(xxx) cancel(a^2) + 2a + cancel(b^2) + 6b cancel(- a^2) + 2a cancel(- b^2) + 6b = -1 - 58#

#rArr 4a + 12b = -59#

#rArr a + 3b = -59/4#......................(v)

Now, Subtract (iii) from (v).

#color(white)(xxx) cancel(a) + 3b cancel(- a) - 2b = -59/4 +4#

#rArr b = -43/4#

Now Putting #b = -43/4# in (iii).......

#a + 2(-43/4) = -4#

#rArr a = -4 + 43/2#

#rArr a =(-8 + 43 )/2#

#rArr a = 35/2#

Finally got the FREAKING Coordinates of #A = (35/2, -43/4)#. Oh Boy, I'm tired.

And, The Co-ordinates of #F# = #((a - 1)/2, (b - 3)/2) = ((35/2 - 1)/2,(-43/4 - 3)/2) = (33/4, -55/8)#

Let the Equation of #AE# be #y = m_1x + c_1#.

To Find the #m_1#, use the Point-Slope Form of the Line.

Point Slope Form = #m = (y_2 - y_1)/(x_2 - x_1)#

So, #m_1 = (1 + 43/4)/(-1/2 - 35/2) = (47/4)/(-18) = -47/72#.

And, #AE# has a point on it, #E#.

So The Equation of #AE# will be satisfied by #x = -1/2, y = 1#.

So,

#color(white)(xxx) y = m_1x + c_1#

#rArr y = -47/72x + c_1#

#rArr 1 = -47/144 + c_1# [Puttig #x = -1/2, y = 1#]

#rArrc_1 = (144 + 47)/144 = 191/144#

So, The Equation of #AE#:- #144y= -47x + 191#.

Similarly, Let the Equation of #DF# be #y = m_2x + c_2#.

Using the Point-Slope Form,

#m_2 = (1+55/8)/(1 - 33/4) = (63/8)/(-29/4) = -63/58#

Now,

#color(white)(xxx)y = (-63/58)x + c_2#

#rArr 1 = -63/58 + c_2# [Putting #y =1, x = 1#]

#rArr c_2 = (58 + 63)/58 = 121/58#

So, The Equation of #DF#:- #58y = -63x + 121#

YESSSSS!!!!!!!! FINALLY!!!!!

I pray to God that this helps.

P dilip_k
Jun 8, 2018

enter image source here

Let #(h,k)# be the coordinates of point #A# of the parallelogram.

So four corner points of the parallelogram becomes

#A->(h,k)#, #B->(-1,-3)#, #C->(-2,1)#, #D->(1,1)#

Diagonals of a parallelogram bisect each other at #O#

So mid point of BD is #((-1+1)/2,(-3+1)/2)->(0,-1)#

So mid point of AC will be #((h-2)/2,(k+1)/2)#

Hence #(h-2)/2=0=>h=2#
And #(k+1)/2=-1=>k=-3#

So coordinates of A is #(2,-3)#

The coordinates of E the mid point of DC becomes

#E->(-1/2,1)#

And the coordinates of F the mid point of AB becomes

#F->(1/2,-3)#

So equation of AE will be

#(y+3)/(x-2)=(1+3)/(-1/2-2)#

#=>8x+5y-1=0#

And the equation of CF becomes

#(y-1)/(x+2)=(1+3)/(-2-1/2)#

#=>8x+5y+11=0#

Related questions
Impact of this question
4630 views around the world
You can reuse this answer
Creative Commons License