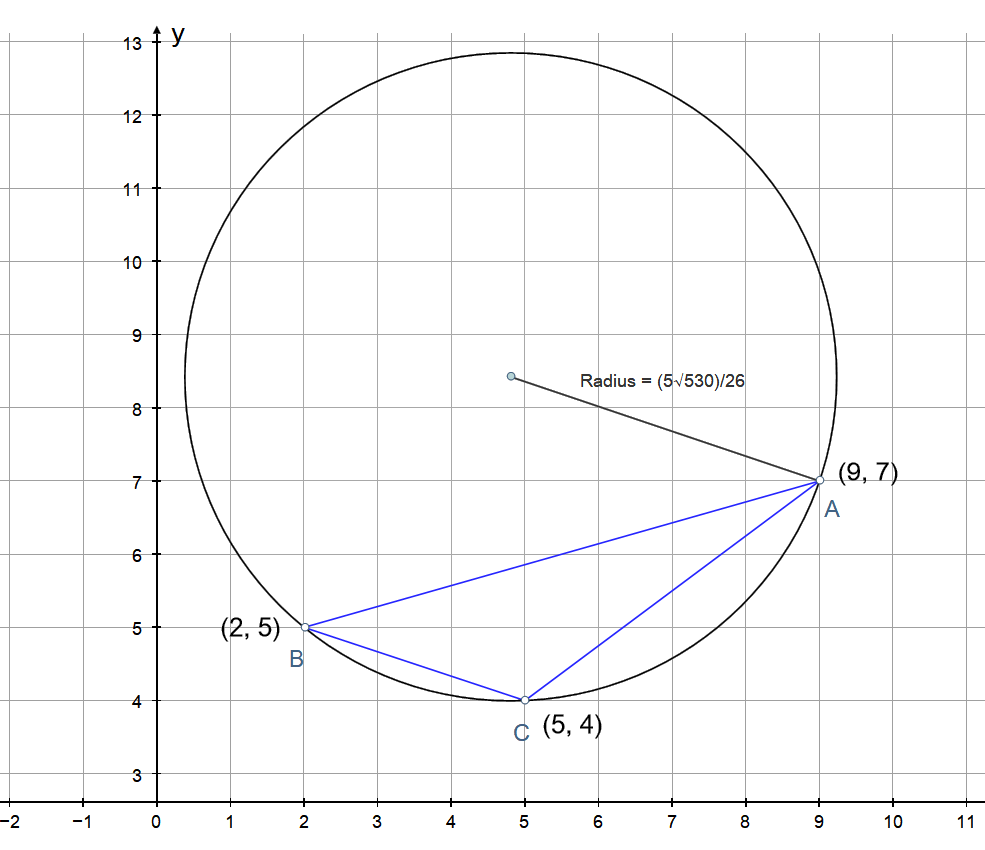
A triangle has corners at #(9 ,7 )#, #(2 ,5 )#, and #(5 ,4 )#. What is the area of the triangle's circumscribed circle?
1 Answer
Explanation:
In order to find the area of the circumscribed circle, we need to find the radius of this circle. It can be shown that:
Where
We can prove this with the following:
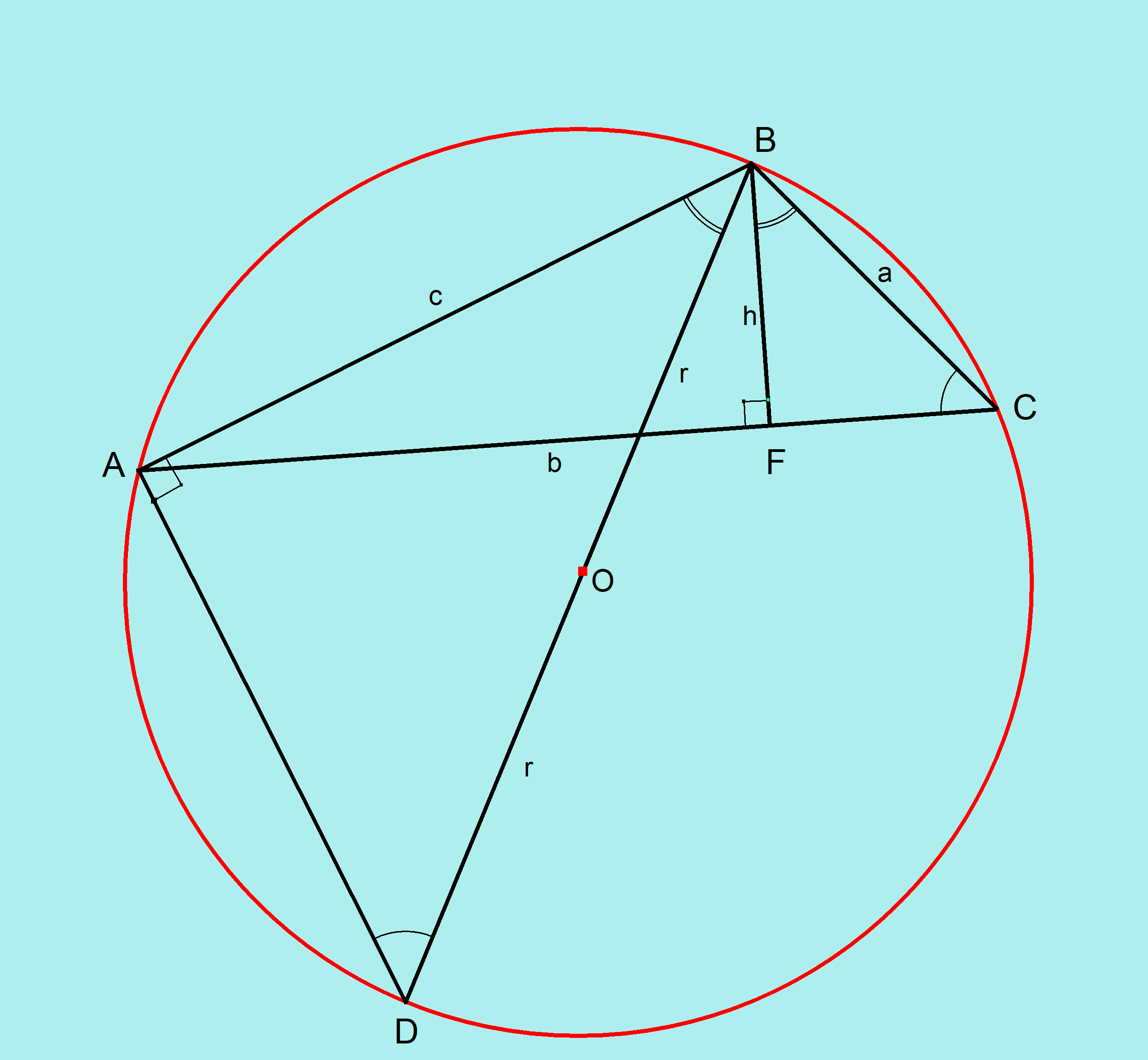
From diagram:
Draw a line from B to D through centre O. Notice that this is the diameter of the circle, and is twice the radius, so we can call this
Let the altitude of
Then area of
The angle subtended at the circumference by the diameter is always a right angle.
These are angles subtended by the same chord AB
Looking at
Using the properties of similar triangles:
Substituting this in
After rearranging we have:
Now we know the radius in terms of the sides and area of
First the sides
Let the given points be:
This gives sides:
For
For
For
Area of
Taking AC as the base, we now find the gradient of this line segment, then we find the equation of the line. We then find the equation of the line perpendicular to this passing through the vertex B.
Gradient of AC:
Using point slope form of a line and vertex
A line perpendicular to this will have gradient:
The line passes through
Using point slope form of a line:
The point of intersection of
Solving simultaneously:
Substituting in
Co-ordinates
Let
We now find the length of
So:
Area of circumscribed circle is:
PLOT: