Who invented Pythagoras theorem?
2 Answers
The theorem was not so much invented as explained.
Pythagoras was the first person to realise why that ratio (amongst others) worked.
Explanation:
The theorem of Pythagoras had been known and used by the people of the ancient civilizations for many years. For example by the Greeks, Romans, Egyptians and Chinese.
This is how the Egyptians managed to get the angles of the pyramids to be exactly
They used a long length of rope marked into
The theorem was not so much invented as explained.
Pythagoras was the first person to realise why that ratio (amongst others) worked.
According to legend, he was visiting a palace in Crete and something in the pattern of the tile mosaic on the floor made him realise that it is the areas of the squares on the sides of the triangle which lead to the result we know as Pythagoras Theorem.
The Old Babylonians beat Pythagoras by over a millennium. Pythagoras is thought (with very little evidence) to have the first proof.
Explanation:
The oldest known instance of folks knowing the Pythagorean Theorem is from the Old Babylonians, around 1800 BC, the time of Hammurabi. The tablet Plimpton 322 is a table of Pythagorean Triples in angle order, increasing by approximately one degree per entry. So it appears the OBs had a fairly well developed trigonometry based on Pythagorean Triples. Unlike ours, it always gave exact answers. The tablet YBC 2789 has an approximation to the square root of two.
It appears the concept of a proof didn't arise until Thales, circa 600 BC. There seem to be conflicting reports as to whether Thales met a young Pythagoras or died 30 years before he was born. Pythagoras' teacher Anaximander is thought to have been Thales' student. Pythagoras or one of the other Pythagoreans is thought to be the first to produce a proof of the Theorem, but the evidence is pretty sketchy. The proof is thought to be along the lines of this animation:
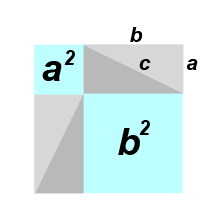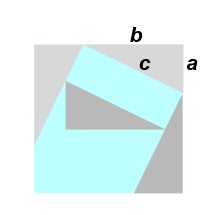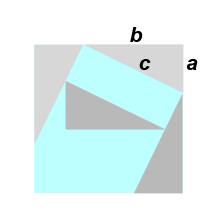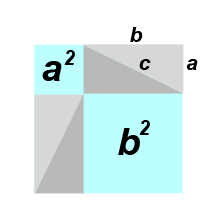
Two hundred years later Euclid of course later published his proof in the Elements, which is much more complicated.
The OB tablet Plimpton 322 is awesome. In the first column the OBs encode an entire Pythagorean Triple as a single decimal (actually sexagesimal, they used base 60) number between 1 and 2. The text above the first column, describing the column’s contents, may be considered a statement of the Pythagorean Theorem. A loose translation is, “the square of the normalized diagonal from which one is subtracted and the square of the normalized width comes up.”
In other words
which is equivalent to the Pythagorean Theorem.

The OBs thought about the diagonal of a rectangle where we think about the hypotenuse of a right triangle. The table is in order from a very squarish rectangle (nearly equal sides) to successively more oblong ones. It’s thought to be a fragment of a longer table used for trigonometry.
The rectangles are normalized so the long side, the length, is one. It’s the long side because the OBs choose triples where
Maybe this odd choice of first column is really in the middle of the tablet. On the other hand, it's the sort key. The table is ordered by decreasing
Let’s decode an example. The first column of the fourteenth row, with the sexagecimal digits rendered in decimal, is
1 25 48 51 35 06 40
The decimal point is implied right after the 1. Like it would be for us, subtracting one from these numbers between one and two just means dropping the leading digit, easy. Here we’re interested in two fractions:
I wrote the numerators in base 60 and the denominators in base 10. These work out to
Our Pythagorean Triple is
Pretty good for no calculators. They also seem to have decimals (uh, sexagesimals) three thousand years before Stevin.


