Differentiate \frac{r}{\sqrt{r^2+5}} ?
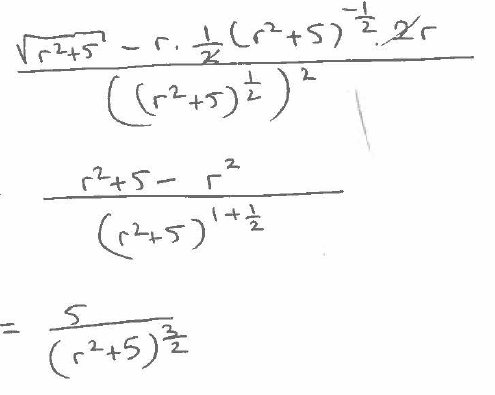
I'm unsure how they went from the first step to the second step? How did the (r^2+5)^(1/2) on the denominator from the first step turn into an exponent of 1 on the second step? Also, how do you get the -r^2 in the numerator in the second step?
I'm unsure how they went from the first step to the second step? How did the
2 Answers
Explanation:
"differentiate using the "color(blue)"product rule"
"given "y=g(h(x))" then"
dy/dx=g(x)h'(x)+h(x)g'(x)larrcolor(blue)"product rule"
"here "y=r/(sqrt((r^2+5)^(1/2)))=r(r^2+5)^(-1/2)
g(r)=r rArrg'(r)=1
h(r)=(r^2+5)^(-1/2)
h'(r)=-1/2(r^2+5)^(-3/2)xxd/(dr)(r^2+5)
color(white)(h'(x))=-1/2(r^2+5)^(-3/2)xx2r=-r(r^2+5)^(-3/2)
(dy)/(dr)=-r^2(r^2+5)^(-3/2)+(r^2+5)^(-1/2)
color(white)((dy)/(dr))=(r^2+5)^(-3/2)[cancel(-r^2)cancel(+r^2)+5]
color(white)((dy)/(dr))=5/(r^2+5)^(3/2)
By expanding by
Explanation:
Your first question can be answered by a simple algebra rule. We know that :
so therefore
In the next step, we expanded the fraction by
Therefore in the denominator we got

