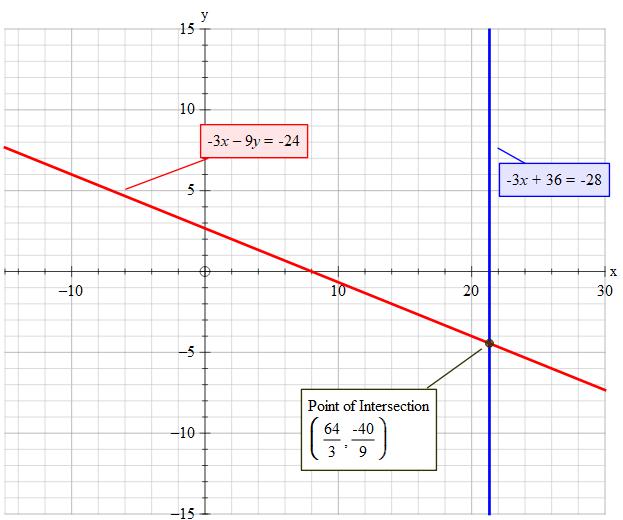
Given:
#-3x+36=-28" "...................Equation(1)#
#-3x-9y=-24" ".....................Equation(2)#
Notice that there is no #y# term in #Eqn(1)#
So this ends up being in the form #x="something"# which is a vertical line (parallel to the y-axis).
#Eqn(2)# can be manipulated into the form of #y=mx+c#
where in this case #m!=0# so the two plots cross. Thus there is a solution (is a 'correct' system -using your words).
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#color(blue)("Solving for shared point- intersection")#
Consider #Eqn(1)#
Subtract 36 from both sides - 'gets' the #x# term on its own
#-3x=-28-36 = -64#
Divide both sides by #-3#. 'gets' the #x# on its own and changes it to positive.
#color(red)(x=+64/3)" ".....................Equation(1_a)#
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
Consider #Eqn(2)#
Substitute for #color(red)(x)#
#color(green)( -3color(red)(x)-9y=-24 color(white)("d")->color(white)("d") [-3color(red)(xx64/3)]-9y=-24 )#
#color(white)("ddddddddddddddd")->color(white)("dddd")-64color(white)("dd.d")-9y=-24#
Add 64 to both sides
#color(white)("ddddddddddddddd")->color(white)("ddddd")-9y= 40#
Divide both sides by #-9#
#color(white)("ddddddddddddddd")->color(white)("dddddd")+y=-40/9#